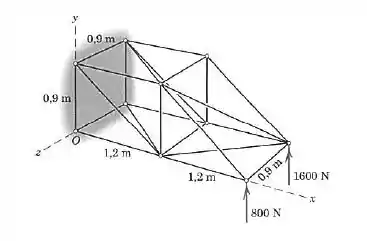
Duas cargas direcionadas para cima são exercidas sobre uma pequena treliça tridimensional. Reduza estas duas cargas a um único sistema força-binário no ponto Mostre que é perpendicular a . Em seguida, determine o ponto no plano pelo qual passa a resultante.

Show de bola. Agora queremos reduzir o sistema a um sistema força-binário equivalente em . Para isso, agora vamos calcular o momento de cada força em relação a .

Veja, antes, disso, que as distâncias dos pontos de aplicação das forças até o ponto , são, respectivamente:

Assim, o momento de cada força será dado por:

Somando os momentos:

Pronto, podemos dizer que o sistema força-binário resultante em relação ao ponto pode ser definido por:

Agora vamos ver se a força resultante é perpendicular ao momento:

Como fazemos isso? Simples, lembra que o produto escalar entre vetores perpendiculares é nulo? Faremos esse produto então:

Escrevendo os vetores com todas as componentes ( as que são zero também):

É isso! Então, os vetores são perpendiculares sim.

Beleza. Agora queremos saber a localização da resultante: Para isso, queremos saber o vetor posição em relação ao ponto

Nós não sabemos quais são as suas componentes, mas sabemos que ela deve estar no plano , o plano horizontal desse problema. Como sabemos? Por duas fontes do enunciado:

Primeiro: todas as forças atuam em pontos do plano .

Segundo: O enunciado te pede pra achar a posição da resultante nesse plano.

Show? Então podemos escrever o vetor assim:

Queremos achar

Pra isso, vamos usar a igualdade:

Podemos usar essa igualdade, sem envolver um torçor, porque a resultante é perpendicular ao momento.

Temos o momento resultante e a força resultante.

Assim:

Desenvolvendo o lado esquerdo:

Agora, comparando com o valor do momento resultante:

Perceba: temos que comparar com e com . Assim:

Assim, o ponto por onde passa a resultante é: