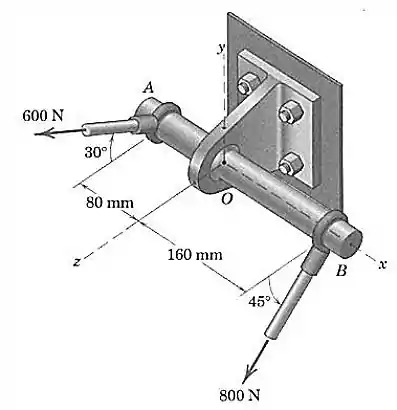
Determine o sistema força-binário em que seja equivalente às duas forças aplicadas ao eixo . é perpendicular a Nesse caso, determine as coordenadas no plano por onde passa resultante do sistema de forças.
Passo 1
Vamos primeiro calcular a resultante das forças. Veja que elas possuem uma característica em comum: ambas fazem um ângulo com o eixo
Podemos definir a força de assim:
Podemos definir a força de assim:
Assim, a força resultante é dada por:
Passo 2
Agora vamos calcular o momento que cada uma faz em relação ao ponto
Perceba que as distâncias são dadas apenas no eixo . Então, vamos fazer o produto vetorial para cada força.
Para a força , o vetor distância é:
Assim, o produto vetorial fica:
Para a força , o vetor distância é:
Então, o produto vetorial fica:
Assim, o momento total em relação ao ponto
Pronto, com a força resultante e esse momento, definimos o sistema força-binário equivalente em
Passo 3
Sendo:
Vamos ver se os vetores são perpendiculares. Para isso, vamos efetuar o produto escalar:
Como o produto é diferente de zero, eles não são perpendiculares.
Assim, podemos representar a resultante por um conjunto torçor.
Vamos escrever a força resultante na forma:
Assim:
Passo 4
Queremos agora achar o ponto onde a resultante pode ser representada, junto com o seu torçor:
Vamos usar, então, a relação:
é o momento do torçor e, portanto, tem a mesma direção que a força resultante:
Passo 5
Vamos desenvolver:
Passo 6
Resolvendo:
Lembrando que isso é igual a
Igualando termo a termo, vamos chegar nas seguintes equações:
Da primeira equação temos
Da segunda podemos tirar que
Substituindo na terceira
Substituindo esse valor de na equação que tem
Assim: