Substitua as três forças que atuam na placa por um torçor. Especifique os vetores força e momento torçor, suas intensidades e o ponto onde sua linha de ação intercepta a placa.
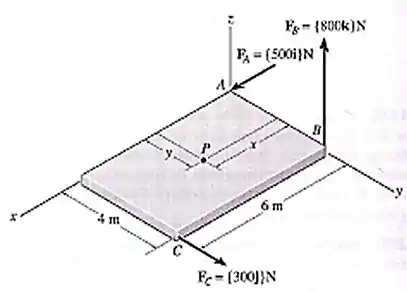
Passo 1
Vamos considerar o ponto como a origem do sistema de coordenadas.
Calculando a força resultante, temos:
Podemos escrever a força assim:
Onde:
Assim:
Passo 2
Vamos calcular o momento que cada força exerce em relação ao ponto
O desta força é momento nulo, já que a sua linha de ação cruza o ponto
Já a outra força:
Ela possui o seguinte vetor posição:
Assim:
E a força:
Possui o vetor posição igual a :
Assim:
Passo 3
Assim:
É o sistema força-binário que representa o sistema. Vamos calcular o produto escalar entre os dois vetores acima pra ver se eles são perpendiculares:
Como é diferente de zero, os vetores não são perpendiculares.
Passo 4
Assim, queremos achar o ponto onde atua o torçor. Para isso, vamos usar a relação:
Onde tem a mesma direção que
Passo 5
Vamos desenvolver o produto
Assim, fazendo a soma disso com
Isso tudo igual ao
Passo 6
Assim, igualando termo a termo:
Da segunda equação, temos que:
Substituindo na primeira e na terceira equação:
Passo 7
Temos esse sistema aqui:
Multiplicando a primeira equação por
Somando com a segunda:
Substituindo isso na primeira equação:
Substituindo em:
Passo 8
Por fim, podemos dizer que o torçor pode ser escrito por:
E que o ponto em que a linha de ação do mesmo cruza o plano é: