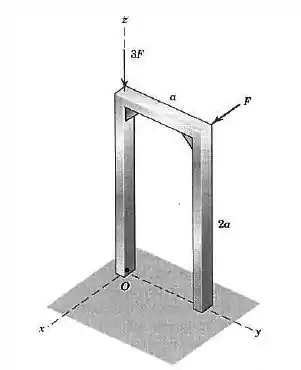
Substitua as duas forças atuando na moldura por um torçor. Escreva na forma vetorial o momento associado com o torçor e especifique as coordenadas do ponto no plano pelo qual passa a linha de ação do torçor. Observe que a força de módulo é paralela ao eixo

Vamos agora calcular o momento resultante das forças em relação a Pra isso, vamos calcular o momento de cada força e depois somar.

Para a força

Como você pode ver, o vetor é paralelo ao vetor força, assim, o produto abaixo é nulo e por isso o momento é nulo:

Para a força

Assim, usando o produto vetorial:

Desenvolvendo:

Assim:

Show de bola. Agora vamos ver se dá para a gente escrever esse sistema como um sistema força-torçor. Para isso, vamos fazer o produto escalar entre a resultante e a resultante

Como é diferente de zero, podemos escrever o sistema como um sistema força-torçor:

Beleza, agora queremos escrever o momento associado ao torçor na forma vetorial e achar o ponto em que a linha de ação do torçor passa.

O que sabemos? Sabemos que o torçor tem a mesma direção que a força resultante. Por isso calculamos antes:

E sabemos que a soma desse momento mais o momento que a força resultante faz em relação ao ponto de origem é igual ao momento resultante em relação à origem:

Queremos achar e o vetor

Vamos antes desenvolver:

Desenvolvendo:

Então:

Voltando àquela igualdade:

Perceba que do lado esquerdo o termo que acompanha é nulo. Assim, do lado esquerdo também precisa ser:

Comparando os outros termos:

Substituindo o valor de

Assim, o valor de é:

Assim, podemos escrever o momento como:

E o ponto