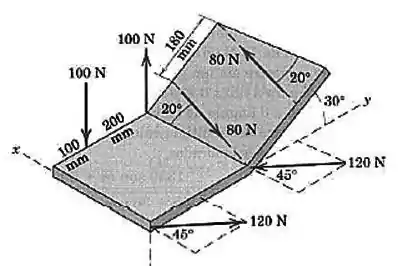
Três binários são formadas por três pares de forças iguais e opostas. Determine a resultante dos três binários.
Passo 1
Beleza, vamos começar identificando cada binário.
O primeiro é esse aqui:
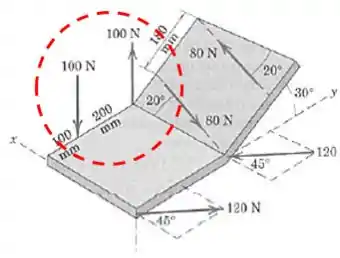
O segundo é:
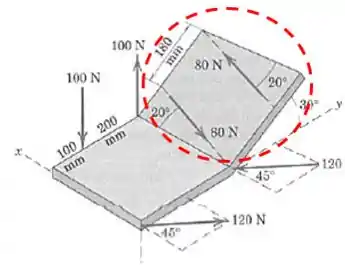
E o terceiro é esse aqui:
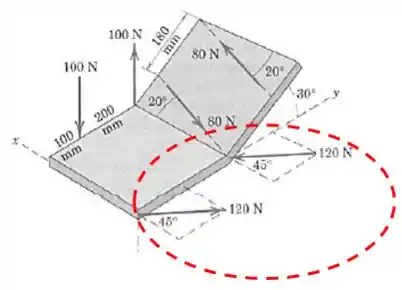
Passo 2
Antes de começarmos a calcular, vamos lembrar de uma coisa: o momento dos binários é o mesmo em qualquer ponto do sistema.
E é por isso que podemos calcular o momento deles só multiplicando o valor da força pela distância entre eles:
É importante notar que essa distância é a distância perpendicular entre os vetores.
E pra achar a direção e o sentido? Bom, aí vamos usar a regra da mão direita. Bora lá.
Passo 3
Vamos começar pelo mais simples, o primeiro binário. Então, o valor do momento é dado por:
As forças de são paralelas ao eixo . Assim, pela regra da mão direita:
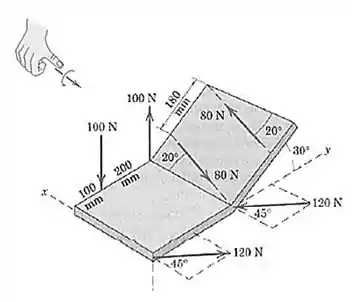
Então:
Passo 4
Vamos fazer agora o terceiro binário.
Nesse aqui temos uma complicação: não temos a distância perpendicular entre as forças. Precisamos usar um pouquinho de trigonometria:
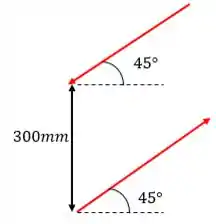
Assim:
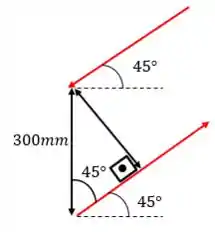
Então, a distância perpendicular entre as forças, em metros, é dada por:
E o momento do binário:
A figura não deixou claro o sentido positivo de , então vamos arbitrar esse aqui:
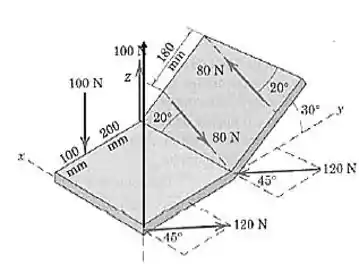
Agora, usando a regra da mão direita:
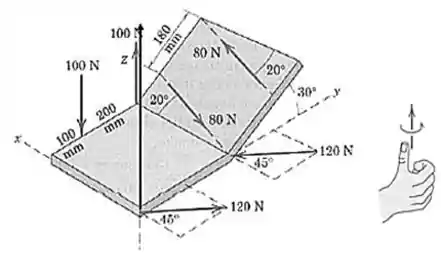
Então, o vetor pode ser dado por:
Passo 5
O segundo binário vai ser mais difícil um cadinho. Veja só: o binário não têm distâncias perpendiculares aos vetores e o plano de giro deles não é ortogonal.
Primeiro vamos lidar com as distâncias:
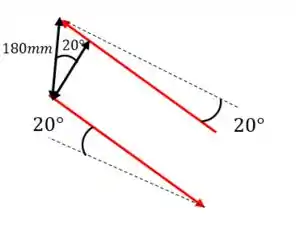
Assim, a distância perpendicular entre as forças vale:
Então, o momento tem módulo:
Antes de calcular, vamos determinar a direção.
Passo 6
A direção a gente determina pela regra da mão direita, mas o plano onde estão as forças não é ortogonal. O que sabemos, no entanto, é que o vetor momento vai ser perpendicular a esse plano:
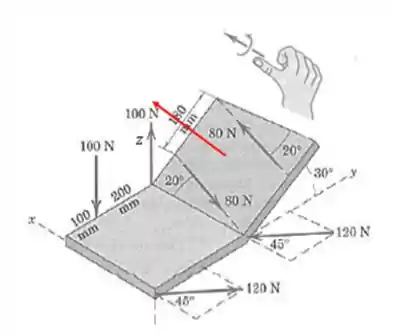
Para saber o vetor direitinho, basta a gente perceber que o plano acima faz um ângulo de com o plano
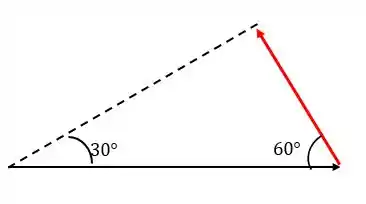
Assim, podemos dizer que o vetor que aponta na direção do vetor momento é dado por:
Por fim, podemos escrever o momento como:
Fazendo as contas:
Passo 7
A soma dos momentos será, então: