Substitua o sistema de forças aplicado nas chapas da figura por um sistema equivalente composto por uma força e um conjugado atuando no ponto . O sistema de forças da figura é composto de binários e uma força.
Atenção: inclua os sinais das componentes de acordo com o sistema de referência dado.
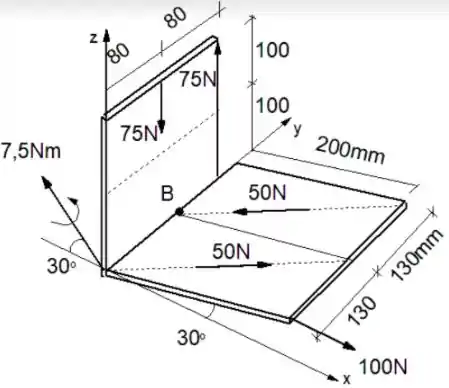
Passo 1
Fala aí, pessoal, como temos uma questão com muitos elementos, então vamos cuidadosamente pensar inicialmente na força resultante, certo? Depois falamos sobre o conjugado!
Começando pelos binários compostos pelas forças :
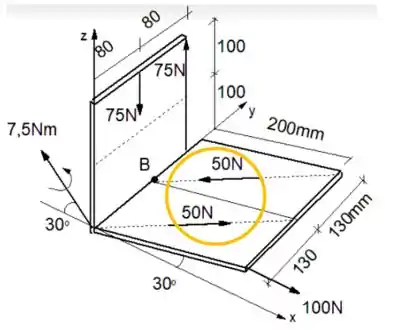
Você concorda comigo que em um binário, as forças tem o mesmo módulo, porém sentidos opostos? Então se formos decompor essas forças em nossos eixos, elas irão se cancelar completamente e não ajudarão em nossa força resultante!
O mesmo ocorre com o binário composto pelas duas forças de :
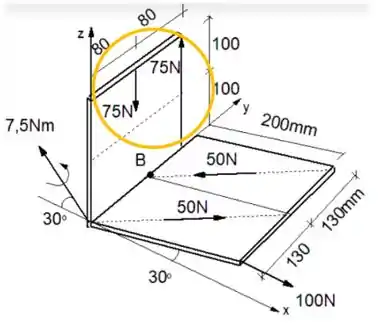
Elas também se cancelam e não somam nada a força resultante!
Por outro lado, olhando para a última força presente em nosso diagrama, vemos a força de na direção positiva de :
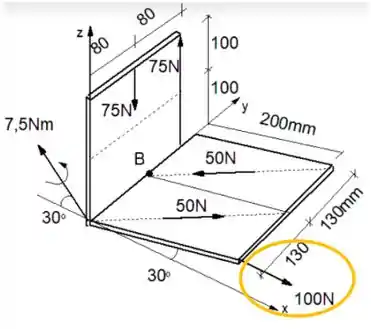
Ela então será a única força que compõe a nossa força resultante, já que todas as outras forças se cancelaram:
Passo 2
Agora que já temos a força resultante, temos que pensar no conjugado resultante, nesse caso vamos analisar cada uma das forças e como elas atuam em nosso ponto de interesse, começando pelo binário composto pelas forças de :
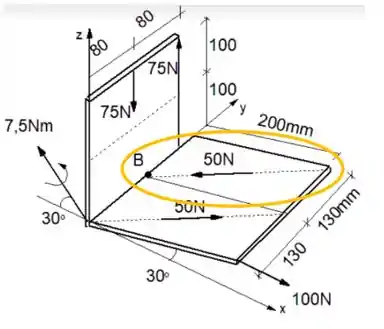
Como a linha de aplicação da força passa pelo ponto , então essa força não gera nenhum conjugado em , pois não existe braço de alavanca para isso.
Enquanto por outro lado, a outra força de tem outro efeito:
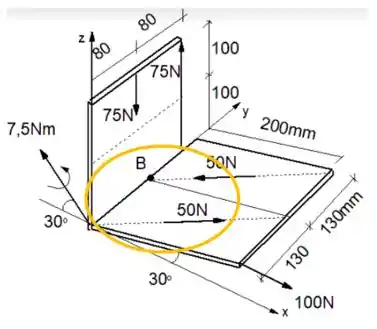
Percebemos que existe um braço de alavanca entre a posição do ponto e a linha de ação da força, veja que o vetor distância é:
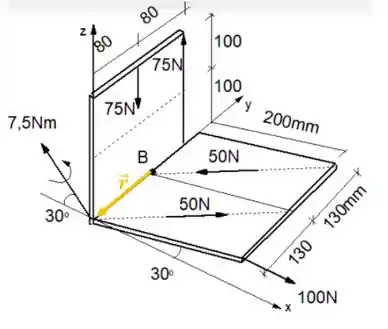
E esse vetor distância tem o tamanho igual a distância entre o ponto e a origem, ou seja, e sentido negativo do eixo :
Mas como sempre operamos em metros e não em milímetros, vamos sempre converter, beleza?
Mas você concorda comigo que devemos decompor essa força de em nossos eixos e , ou seja, temos que fazer uma proporção entre os tamanhos da placa:
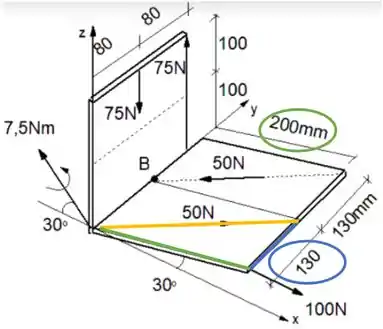
E não esquece que esse plano ta inclinado para cima em :
Vamos aplicar agora o produto vetorial para encontrar o conjugado produzido por essa força:
Passo 3
Vamos calcular o momento causado pelas forças de , começando por:
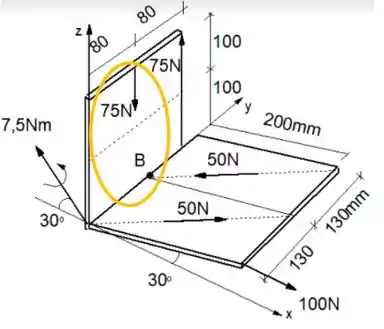
Olhando de frente, percebemos que a linha de atuação da força não é a mesma que o ponto :
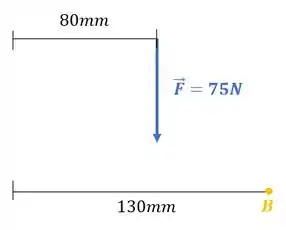
Logo nosso vetor distância entre o ponto e a linha de atuação da força, temos:
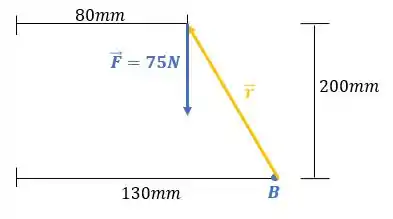
O tamanho do vetor é a diferença entre:
Agora considerando que a distância é contrária ao eixo , então:
Como a força aplicada é:
Então nosso produto vetorial para encontrar o segundo conjugado é:
Passo 4
Já fizemos a primeiro conjugado do binário de , vamos então para a segunda força:
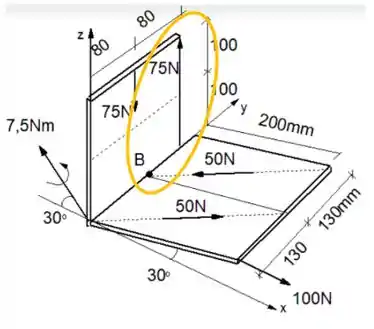
Olhando de frente, vamos ver o vetor distância entre a força e o ponto :
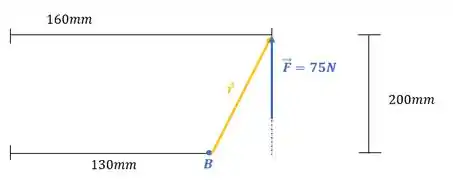
Onde o vetor distância é:
Como a força aplicada é:
Então nosso produto vetorial para encontrar o segundo conjugado é:
Passo 5
O último conjugado que temos que considerar é o que já existe no nosso diagrama:
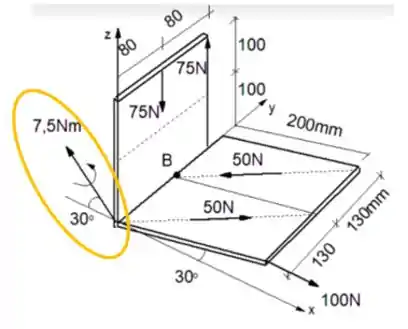
Vamos decompor esse conjugado nas direções e :
Passo 6
O último passo é somar todas essas componentes:
Substituindo os valores que encontramos nos últimos passos:
Então:
Chegamos no final dessa pergunta então!