Durante uma perfuração, o pequeno dispositivo robótico é submetido a uma força de no ponto , como mostrado. Substitua esta força por um sistema força-binário equivalente no ponto
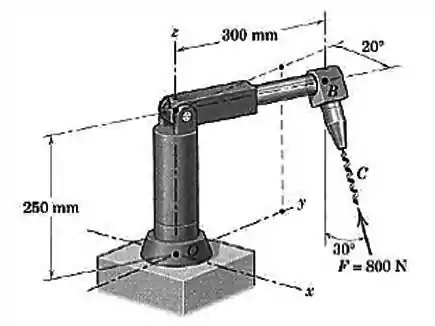
Passo 1
Vamos começar a questão escrevendo a força de em termos de vetores e , ou seja, em componentes e
Primeiro perceba que a componente é a mais fácil de encontrar. Na figura dá pra ver que a força de faz um ângulo de com o eixo
Então, vamos ficar com isso aqui para a componente :
Passo 2
Para achar as componentes e , primeiro perceba que a componente no plano horizontal da força é dada por:
Agora precisamos decompor essa força novamente em relação ao ângulo de e, então, conseguiremos as componentes que queríamos:
Assim:
Passo 3
Agora vamos achar o vetor , ou seja, o vetor distância entre o ponto e a origem.
Vamos primeiro olhar a distância vertical: Fica claro que ela é dada por:
Pra achar as componentes e , basta percebermos que essas são projeções do segmento
Assim:
Show de bola? Estamos prontos pra usar:
Passo 4
Então:
Efetuando os determinantes:
Passo 5
Show de bola! Então podemos dizer que o sistema de forças pode ser representado por um sistema força-binário equivalente dado pelos vetores: