Em um bairro existem mil residências que podem ser atendidas por empresas de TV a cabo. A empresa tem assinantes, a empresa tem e a empresa tem assinantes, sendo que algumas residências em condomínios subscrevem aos serviços de mais de uma empresa. Assim, temos residências que são assinantes de e , de e , de e e que são assinantes das três empresas. Se uma residência desse bairro é sorteada ao acaso, qual é a probabilidade de:
- Ser assinante apenas da empresa ?
- Assinar pelo menos uma delas?
- Não ter TV a cabo?
Passo 1
Temos um total de residências que podem ser atendidas por três empresas de TV diferentes .
Vamos anotar os dados que o problema dá:
Esses são os totais de usuários de cada empresa... mas também temos usuários que usam serviços de mais de uma empresa. Esses valores nos dão:
Passo 2
Pra facilitar a gente a resolver todos os itens, vamos usar aquela ideia de conjuntos?
Vamos ter três conjuntos, um pra cada empresa, e já conhecemos todas as interseções.
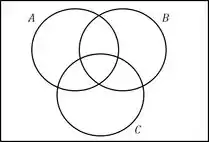
Para preencher começamos pela interseção entre as três empresas que vale e depois pelas interseções entre duas (descontando o ) e por fim pro valor total de assinantes de cada empresa (sem esquecer de descontar todas as interseções).
Por fim, ficamos com isso aqui:
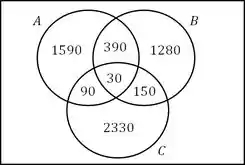
Passo 3
(a)
Olhando no nosso esquema de conjuntos, a gente vê que só residências são assinantes somente da empresa .
Então a probabilidade da escolhida ser assinante só de é:
Lembrando que é o total de residências.
Passo 4
(b)
Pra achar essa probabilidade, a gente precisa encontrar o número total de pessoas que assinam, certo? Afinal de contas, a probabilidade de pelo menos uma pessoa assinar é a probabilidade de ocorrerem assinaturas. Pra encontrar esse número, podemos somar todos os números que aparecem no nosso esquema de conjuntos ou utilizar a fórmula da união de conjuntos. Assim:
Mas veja, podemos obter essa resposta também usando:
E daí a probabilidade será:
Passo 5
(c)
Se o nosso esquema representa as residências que tem pelo menos uma TV à cabo, pra saber o total de residências sem nenhuma, é só fazer...
E daí a probabilidade vai ser:
Você poderia pensar também que:
E isso a gente tinha calculado antes:
Daí: