Considere o quadrado com vértices (0,0), (1,0), (0,1) e (1,1). Suponha que a probabilidade de uma região A (evento) seja a área dessa região.
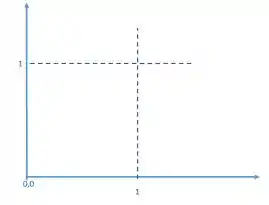
a) Represente graficamente o evento A = conjunto dos pontos cuja distância à origem seja menor ou igual a 1.
b) Calcule P(A)
c) Calcule a probabilidade do evento , onde b é um número tal que
d) Calcule , onde B foi definido em (c).
Passo 1
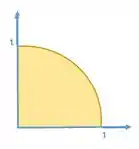
a)Represente graficamente o evento A = conjunto dos pontos cuja distância à origem seja menor ou igual a 1.
Pelo enunciado podemos notar que a região que delimita o evento A é uma curva, um segmento de circunferência, cujo evento A é toda área delimitada por essa curva.
Passo 2
b) Determine P(A)
Após entendermos quem é A, a probabilidade de A ocorrer será:
Onde utilizaremos a área como referência.
A área da região A é um quarto da área de uma circunferência de raio 1 e a área total é a área de um quadrado de lado 1.
Passo 3
c) Calcule a probabilidade do evento , onde b é um número tal que
Primeiramente vamos entender quem é esse evento B com uma figura:
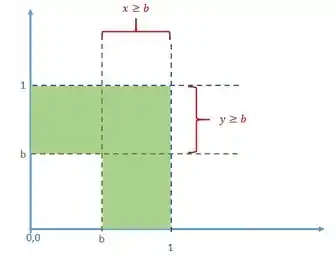
A área de vai ser essa área verde.
Repare que a área branca que restou embaixo à esquerda vale . Ou seja, como a área do quadrado vale , a área verde vale . Assim:
Passo 4
d) Calcule , onde B foi definido em (c).
Temos simplesmente
Que é justamente aquela área que calculamos antes, do quadrado branco que está embaixo à esquerda na figura.
Resposta
a)
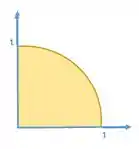
b)
c)
d)