Retira-se uma carta de um baralho. Qual a probabilidade da carta retirada ser uma dama ou uma carta de copas?
Passo 1
Definir os eventos:
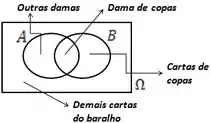
O que queremos?
Probabilidade de ser um ou outro.
Sabemos que:
Passo 2
Determinar e
Se você não se lembra bem, um baralho é composto por 52 cartas, divididas em 4 naipes (espadas, copas, paus e ouros). Cada um desses naipes possui 13 cartas, (às, 1, 2, 3..., 10, dama, valete e rei). Então temos 4 damas totais em um baralho, uma de cada naipe.
Como são 4 damas em 52 cartas,
Como cada naipe possui 13 cartas,
E:
Lembrando que a interseção é a dama de copas.
Passo 3
Substituir na fórmula inicial.
Resposta
Exercícios de Livros Relacionados
Um lote de 140 pastilhas (chips) semicondutoras é inspecionado, escolhendo-se uma amostra de cinco pastilhas. Suponha que 10 das pastilhas não obedeçam aos requerimentos dos consumidores.Quantas amost
Encontrando a probabilidade do complemento de um evento A distribuição etária dos moradores de San Ysidro, Novo México, encontra-se na tabela a seguir. Nos exercícios 47 a 50, encontre a probabilidade
A, B e C são três eventos de um mesmo espaço amostral, tais que: P B = 0,5 P C = 0,3 P B C = 0,4e P A B ⋂ C = 0,5 . Calcule P ( A⋂ B⋂ C ) .
Verifique que para dois eventos quaisquer, A1 e A2, temos que P A 1 ∪ A 2 ≤ P A 1 + P A 2 e que essa relação pode ser usada para n eventos.
Encontrando a probabilidade do complemento de um evento A distribuição etária dos moradores de San Ysidro, Novo México, encontra-se na tabela a seguir. Nos exercícios 47 a 50, encontre a probabilidade