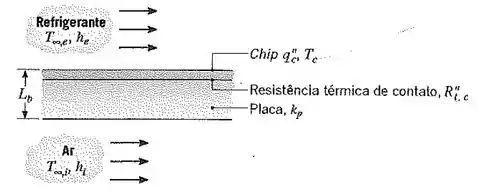
(Adaptada) Aproximadamente componentes elétricos discretos podem ser colocados em um único circuito integrado (chip), com uma dissipação térmica na ordem de . O chip, que é muito fino, tem a sua superfície externa exposta a um líquido dielétrico com e , e a sua superfície interna está conectada à placa de circuito.
A resistência térmica de contato entre o chip e a placa é de , e a espessura e a condutividade térmica da placa são e , respectivamente. A outra superfície da placa está exposta ao ar ambiente, no qual e .
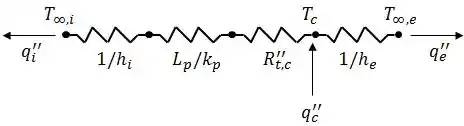
Esboce o circuito térmico equivalente para condições de regime estacionário. Usando as variáveis, identifique as resistências apropriadas, as temperaturas e os fluxos térmicos.
Sob condições de regime estacionário nas quais um fluxo térmico dissipado no chip é , qual é a temperatura do chip?
Passo 1
Esboce o circuito térmico equivalente para condições de regime estacionário. Usando as variáveis, identifique as resistências apropriadas, as temperaturas e os fluxos térmicos.
O circuito térmico é caracterizado por resistências térmicas em série, onde temos um fluxo de calor sendo adicionado circuito pelo chip e fluxos de calor e sendo retirados do circuito pelas convecções realizadas pelo ar e pelo refrigerante.
Dessa forma, o circuito térmico vai ter essa cara:
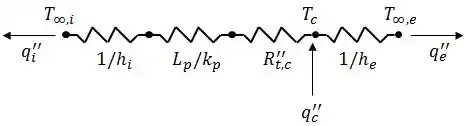
Passo 2
Sob condições de regime estacionário nas quais um fluxo térmico dissipado no chip é , qual é a temperatura do chip?
Fazendo o balanço de energia, vemos que:
Para calcular vamos considerar todas as resistências térmicas à esquerda do chip, e para calcular vamos considerar todas as resistências térmicas à direita do chip.
Dessa forma, teremos o seguinte:
Onde:
Substituindo os valores:
Agora é só arrumar a bagunça:
Resposta