Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos Térmicos

Ver Teoria
Exercício 141234567891011121315

Enunciado

Considere uma parede composta que inclui um painel lateral em madeira dura k m = 0,094   W / m K com 8   m m de espessura; travessas de suporte em madeira dura k t = 0,16   W / m K com dimensões de 40   m m por 130   m m , afastadas com 0,65   m de distância (centro a centro) e com espaço livre preenchido com isolamento k i = 0,038   W / m K à base de fibra de vidro (revestida de papel, 28   k g / m 3 ); e uma camada de 12   m m de painéis de gesso k g = 0,17   W / m K (vermiculita).

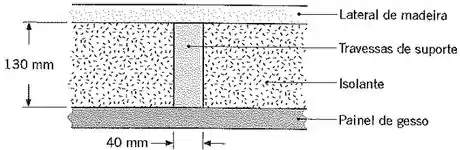
Qual é a resistência térmica associada a uma parede com 2,5   m de altura e 6,5   m de largura (possuindo 10 travessas de suporte, cada uma com 2,5   m de altura)?

Passo 1

A ideia aqui é a seguinte: como cada travessa está afastada centro a centro de 0,65   m , vamos considerar uma unidade da parede da seguinte forma:

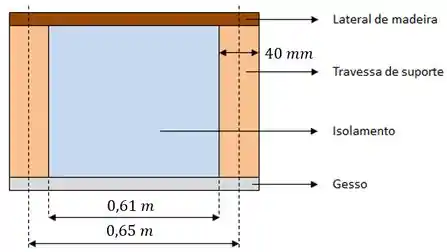
Então vamos começar calculando a resistência térmica total dessa unidade, e a resistência térmica total será dada pela resistência em paralelo de unidades dessa (correspondente a 10 suportes).

Passo 2

Após passar pela madeira, parte do fluxo de calor flui pelo isolamento, e parte flui pela travessa de madeira. Dessa forma, o circuito térmico para esse sistema é dado por:

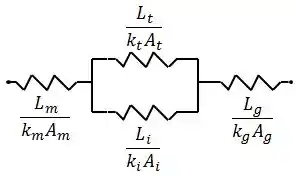
Então vamos começar calculando cada resistência térmica, beleza? Vamos numa batida só:

R m = L m k m A m = 0,008 0,094 × 0,65 × 2,5

R m = 0,0524   K / W

R t = L t k t A t = 0,13 0,16 × 0,04 × 2,5

R t = 8,125   K / W

R i = L i k i A i = 0,13 0,038 × 0,61 × 2,5

R i = 2,243   K / W

R g = L g k g A g = 0,012 0,17 × 0,65 × 2,5

R g = 0,0434   K / W

Passo 3

Para calcular a resistência térmica total dessa unidade, vamos começar calculando a resistência térmica em paralelo R p a r :

1 R p a r = 1 R t + 1 R i

R p a r = R t . R i R t + R i = 8,125 × 2,243 8,125 + 2,243

R p a r = 1,758   K / W

Dessa forma, a resistência térmica da unidade é dada por:

R T , 1 = R m + R p a r + R g = 0,0524 + 1,758 + 0,0434

R T , 1 = 1,854   K / W

Passo 4

Show de bola! Mas a resistência que encontramos é a resistência de apenas uma unidade. A resistência térmica total será dada considerando um circuito em paralelo formado por 10 unidades dessa lado a lado, logo:

1 R T = 1 R T , 1 + 1 R T , 1 + 1 R T , 1 + 1 R T , 1 + 1 R T , 1 + 1 R T , 1 + 1 R T , 1 + 1 R T , 1 + 1 R T , 1 + 1 R T , 1 = 10 R T , 1

R T = 1,854 10

R T = 0,1854   K / W

Resposta

R T = 0,1854   K / W

Exercícios de Livros Relacionados

31 - Um furo de diâmetro D = 0,25m é perfurado através do centro de um bloco sólido de seção transversal quadrada com w= 1m de lado. O furo atravessa o comprimento do bloco, que é de λ = 2m . O bloco
27 - Um fluido quente escoa através de canais circulares em uma peça de ferro fundido (A) com espessura L A = 30m m , que apresenta um contato deficiente com as placas de cobertura (B), que têm espess
26 - Um forno cúbico para fusão de vidro tem dimensões externas de W = 5m de lado e é construído com tijolos refratários, com espessura L = 0,35m e condutividade térmica k = 1,4W / ( m · K ) . As late
Um material nanolaminado é fabricado com um processo de deposição de camada atômica, que resulta em uma série de camadas alternadas empilhadas de tungstênio e óxido de alumínio, cada camada com δ = 0,
Ouro é comumente utilizado no empilhamento de semicondutores para formar interconexões que transportam sinais elétricos entre diferentes dispositivos no conjunto. Além de ser um bom condutor elétrico,