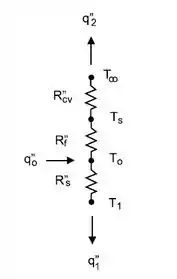
Em um processo de fabricação, um filme transparente está sendo fixado a um substrato, conforme mostrado no esquema. Para curar a fixação a uma temperatura , uma fonte radiante é utilizada para fornecer um fluxo de calor (), que é totalmente absorvido pela superfície fixada. A parte posterior do substrato é mantida a enquanto a superfície livre do filme é exposta ao ar a e um coeficiente de transferência de calor por convecção .
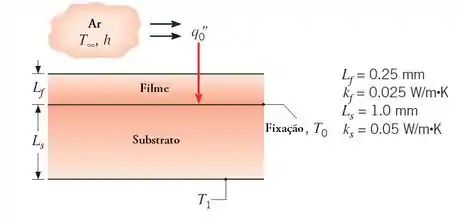
Mostre o circuito térmico representando a situação de transferência de calor em regime estacionário. Identifique todos os elementos, nós e as taxas de calor. Deixe na forma simbólica.
Considere as seguintes condições: , e . Calcule o fluxo de calor necessário para manter a superfície fixada a .
Passo 1
Mostre o circuito térmico representando a situação de transferência de calor em regime estacionário. Identifique todos os elementos, nós e as taxas de calor. Deixe na forma simbólica.
Pra montar um circuito térmico, temos antes que identificar as temperaturas em cada superfície e quais as resistências que existem entre elas: se é de condução, de convecção ou de radiação.
A situação ilustrada pode ser esquematizada da seguinte maneira:
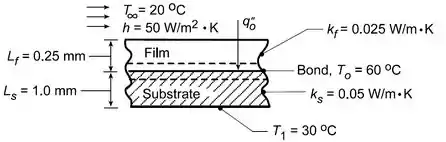
Então, já identificamos quais são as temperaturas do sistema e conseguimos ver que parte do calor é transferido por condução através do substrato () para a parte de baixo e parte dele é transferido para cima, primeiro por condução no filme () e depois por convecção () para o meio fluido.
Dessa forma, ficamos com o seguinte circuito térmico:
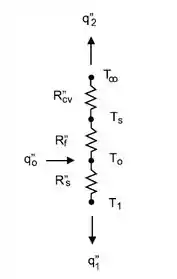
Em que:
- representa a resistência térmica por convecção em .
- representa a resistência térmica por condução no filme em .
- representa a resistência térmica por condução no substrato em .
Passo 2
Considere as seguintes condições: , e . Calcule o fluxo de calor necessário para manter a superfície fixada a .
Agora, bora resolver o problema de verdade, usando os dados fornecidos pelo enunciado. Antes de tudo, a gente tem que calcular cada uma das resistências térmicas:
Note que estamos calculando as resistências a partir do fluxo e por isso a área do filme e do substrato não entram na fórmula.
Como o fluxo de calor de até passa por duas resistências, a gente pode calcular a resistência térmica equivalente () desse trecho e, como essas resistências estão em série, basta somar uma com a outra:
Analisando o circuito, a gente pode ver que parte da energia que entra () sai por cima () e parte dela sai por baixo (). Então, podemos escrever que:
Escrevendo os fluxos em função das resistências:
Resposta