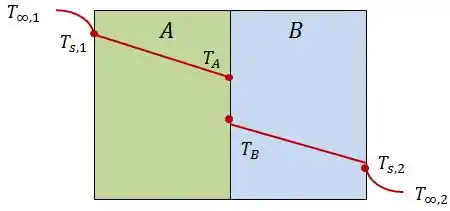
Considere uma parede plana composta constituída por dois materiais com condutividades térmicas e e espessuras e . A resistência térmica de contato na interface entre os materiais é conhecida, sendo .
O material está em contato com um fluido a com e o material está em contato com um fluido a , no qual .
Qual é a taxa de transferência de calor através de uma parede que tem de altura e de largura?
Esboce a distribuição de temperaturas.
Passo 1
Qual é a taxa de transferência de calor através de uma parede que tem de altura e de largura?
O circuito térmico nesse caso será constituído por resistências térmicas em série, onde o calor é transferido do material (que está em contato com o fluido a maior temperatura) para o material (que está em contato com o fluido a menor temperatura).
Dessa forma:

Opa! Conhecemos e . Para calcular a taxa de transferência de calor , podemos usar a resistência térmica total desse circuito da seguinte forma:
Então partiu calcular a resistência térmica total.
Passo 2
Como todas as resistências térmicas estão em série, temos que:
Onde:
Substituindo os valores:
Passo 3
Agora estamos prontos pra calcular a taxa de transferência de calor:
Onde:
Substituindo os valores:
Passo 4
Esboce a distribuição de temperaturas.
Olhando novamente para o nosso circuito térmico:

O nosso trabalho agora é determinar as temperaturas , , e . Então vamos fazer isso tudo num embalo só, beleza?
Dessa forma, a distribuição de temperatura terá essa cara:
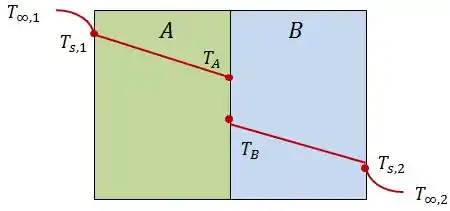
Resposta