(Adaptado) Em uma casa muito distante, uma parede foi construída, composta de camadas de madeira (face externa a casa), isolamento à base de fibra de vidro e placa de gesso (face interna da casa). Em um dia frio de inverno a temperatura no exterior é de e os coeficientes de película internos e externos são e .
A área total da parede é de . Sabendo que a camada de madeira possui de espessura, a fibra de vidro possui originalmente de espessura e a placa de gesso possui de espessura.
Determine, nessas condições, qual a quantidade de calor trocada com o ambiente, sabendo que a temperatura interna será de .
Qual a espessura que a placa de fibra de vidro deve ter para diminuir em 50% a troca térmica?
Passo 1
Determine, nessas condições, qual a quantidade de calor trocada com o ambiente, sabendo que a temperatura interna será de .
A taxa de transferência de calor será dada por:
Onde é a resistência térmica total do sistema, dada por:
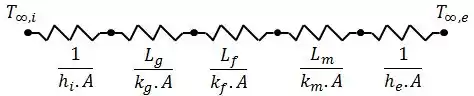
Onde o índice corresponde à região interna, o índice corresponde ao gesso, o índice corresponde à fibra de vidro, o índice corresponde à madeira, e corresponde à região externa.
Assim:
De acordo com a tabela A.3 do Incropera:
Substituindo os valores:
Passo 2
Qual a espessura que a placa de fibra de vidro deve ter para diminuir em 50% a troca térmica?
Agora, queremos descobrir para que seja igual a (metade do valor que encontramos na letra ).
Do passo anterior, temos que:
Reorganizando a equação acima pra isolar o , teremos o seguinte:
Substituindo os valores:
Resposta