Uma casa tem uma parede composta de madeira, isolamento de fibra de vidro e placas de gesso, conforme indicado no esquema. Em um dia frio de inverno, os coeficientes de transferência de calor por convecção são e . A área total da superfície da parede é de . Admita que: , e .
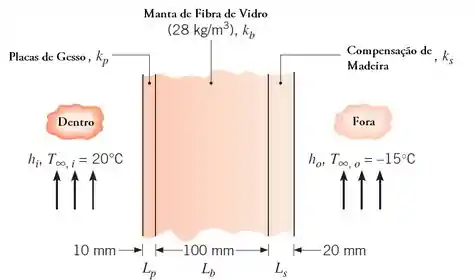
Determine uma expressão que simbolize a resistência térmica total da parede, incluindo os efeitos da convecção interna e externa para as condições dadas.
Determine a perda total de calor através da parede.
Se o vento estivesse soprando violentamente, aumentando para , determine o percentual do aumento da perda de calor.
Qual a resistência que controla o fluxo de calor total através da parede?
Passo 1
Determine uma expressão que simbolize a resistência térmica total da parede, incluindo os efeitos da convecção interna e externa para as condições dadas.
A primeira coisa que temos que fazer é montar o circuito térmico, para identificar as temperaturas e resistências em cada trecho do sistema.
Então, temos que:
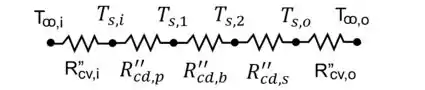
No circuito, a gente pode ver as resistências de convecção nas duas extremidades e as 3 resistências de condução, uma para cada material. Como todas as resistências estão em série, basta somarmos as expressões para simbolizar a resistência térmica total:
Ou podemos ainda representar a resistência térmica total sem unidade de área:
Passo 2
Determine a perda total de calor através da parede.
Agora temos que calcular a perda de calor através da parede composta. Então, precisamos calcular a taxa de calor que sai de dentro () para fora ():
Então, a gente precisa calcular a resistência térmica total (). Sabemos que:
Então:
Substituindo os valores do enunciado:
Então, a gente pode encontrar a resistência térmica total dividindo pela área:
Assim:
Agora a gente já pode calcular a taxa de calor:
Passo 3
Se o vento estivesse soprando violentamente, aumentando para , determine o percentual do aumento da perda de calor.
Se o coeficiente de convecção externo () mudar, a resistência total também vai alterar e assim teremos:
Assim:
A nova taxa de calor será dado por:
Passo 4
Podemos calcular a razão entre as taxas de calor () da seguinte forma:
Ou seja, a perda de calor na situação de ventos mais fortes é maior que a perda de calor nos dias mais calmos. Como a diferença foi tão pequena, mesmo aumentando o coeficiente externo , já sabemos que a resistência de convecção não é a mais relevante.
Passo 5
Qual a resistência que controla o fluxo de calor total através da parede?
Já vimos que a resistência de convecção não é a limitante, então bora verificar as resistências por condução:
Com isso, a gente consegue ver que a resistência limitante é referente à camada de fibra de vidro ().
Resposta
O circuito pode ser ilustrado da seguinte forma:
A perda de calor total equivale a: .
A perda de calor na situação de ventos mais fortes é 0,46 % maior.
A resistência que controla/limita a taxa de calor é a resistência térmica de condução no material B: