(Adaptada) Considere uma camada da pele humana exposta para a atmosfera ao redor. Considere uma camada de tecido gorduroso que possua de espessura e cuja superfície interna seja mantida a uma temperatura de . Em um dia calmo, o coeficiente de tranferência de calor por convecção na supeffíce externa é de , mas com ventos de ele cheg a . Em ambos os casos, a temperatura do ar ambiente é de .
Dado: .
Qual é a razão entre as perdas de calor (por unidade de área da pele) em um dia calmo e em um dia de vento?
Qual será a temperatura da superfície externa da pele em um dia calmo? E em um dia de vento?
Qual a temperatura que o ar deveria ter no dia calmo para causar a mesma perda de calor que ocorre com a temperatura do ar no dia em que há vento?
Passo 1
A situação do enunciado pode ser esquematizada da seguinte forma:
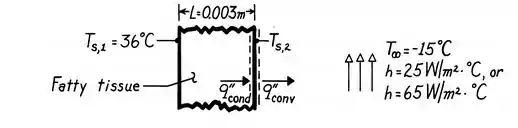
Vendo o esquema, você consegue prever qual o sentido do fluxo de calor? A temperatura interna da pele () é maior do que a temperatura do ar (), então a gente espera que o fluxo saia da pele para o ar!

Essa energia térmica é transferida por dois mecanismos: primeiro por condução na pele e depois por convecção para o ar. Beleza! Como existem dois mecanismos de transferência em série, seria legal representarmos o circuito térmico. Então, se liga aí:
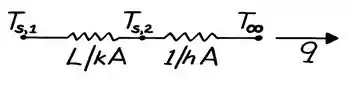
No circuito, a gente já consegue identificar quais são as temperaturas de cada superfície (interna e externa) e a temperatura do fluido (ar), além das resistências de condução e de convecção.
O enunciado pede a relação entre as perdas de calor por unidade de área da pele, ou seja, isso é o que a gente chama de fluxo de calor (). Com base no circuito, a gente tem que:
Como as resistências estão em série, basta somarmos a resistência de condução com a de convecção:
Ótimo! A gente já sabe e e ainda podemos calcular a resistência por condução (). A única variável que a gente vai mudar de uma situação pra outra é a , porque ela depende do coeficiente de convecção ().
Passo 2
Qual é a razão entre as perdas de calor (por unidade de área da pele) em um dia calmo e em um dia de vento?
Então, a gente precisa calcular as resistências térmica de convecção () pro dia calmo e pro dia de vento.
A resistência de condução é dada por:
Logo:
- Para o dia calmo, a gente tem que:
Assim:
Com a resistência calculada, a gente pode calcular o fluxo de calor com:
Passo 3
- Para o dia de vento, a gente tem que:
- Para o dia calmo, a gente tem que:
- Para o dia de vento, a gente tem que:
Assim:
Com as resistência, o fluxo será:
Dess forma, a razão entre entre as perdas de calor (por unidade de área da pele) em um dia calmo e em um dia de vento () será:
Logo:
Isso quer dizer que a perda de calor num dia calmo equivale a da perda de calor observada em um dia de vento.
Isso condiz com o mecanismo físico, porque quanto maior a velocidade do fluido, mais fluido passa em uma região para roubar calor em cada intervalo de tempo, então maior é a convecção.
Passo 4
Qual será a temperatura da superfície externa da pele em um dia calmo? E em um dia de vento?
Bora lembrar do nosso esquema aqui embaixo:
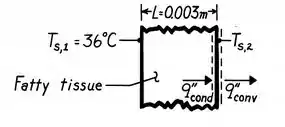
Fazendo um balanço de energia na superfície externa da pele, a gente nota que:
Logo, a gente conclui que:
Em termos das resistências térmicas:
Então, a gente sabe que o fluxo de calor de condução é igual ao de convecção, que é igual ao fluxo total, porque a quantidade de energia témrica que passa pelo circuito em determinado tempo é a mesma!
Então, a gente pode escrever o seguinte:
Isso significa que, pra calcular a temperatura da superfície externa, a gente não precisa fazer no trecho todo, só em um dos trechos: no de condução ou de convecção.
Vou escolher aqui fazer na condução, porque ela não muda de uma situação pra outra, mas tanto faz, tá bem? Mas tanto faz! ^^
Isolando a temperatura da superfície externa (), temos que:
Substituindo os valores que calculamos na letra a), para o dia calmo, temos:
Passo 5
Isolando a temperatura da superfície externa (), temos que:
Substituindo os valores que calculamos na letra a), para o dia de vento, temos:
Passo 4
Qual a temperatura que o ar deveria ter no dia calmo para causar a mesma perda de calor que ocorre com a temperatura do ar no dia em que há vento?
Bom, agora a gente tem comparar duas situações: o dia de vento com o ar a e o dia calmo com o ar a uma temperatura de . Em ambas as situações a pele continua com sua superfície a .
Então, bora calcular que temperatura faz com que a perda de calor no dia calmo seja igual a do dia com vento!
Já vimos que o fluxo de calor no dia de vento com a temperatura do ar a equivale a:
Então, igualando com a expressão para o fluxo no dia calmo, teremos:
Isolando a temperatura do ar , teremos:
Já calculamos a resistência térmica de condução e a de convecção para o dia calmo:
Dessa maneira, substituindo os valores:
Logo, a temperatura que o ar deveria ter no dia calmo para causar a mesma perda de calor que no dia em que há vento equivale a aproximadamente .
Resposta