Considere o plano com o sistema cartesiano canônico e faça uma rotação de um ângulo obtendo um novo sistema . Seja um ponto do plano.
a) Se no sistema , encontre as coordenadas de no sistema .
b) Transforme a equação para o sistema .
Passo 1
Vimos que a relação entre o sistema e o sistema pode ser dada por
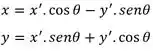
Então, sabendo , vamos utilizer essa relação para resolver os dois itens.
Passo 2
a) Substituindo o ponto , e na relação do passo 1, temos:
Resolvendo esse sistema, encontramos que e .
Então o ponto (ponto no sistema ) é .
Passo 3
b) Temos que
Basta substituirmos essa relações de e em para obtermos essa equação no sistema . Assim:
Resposta
a)
b)
Exercícios de Livros Relacionados
No exercício 7, verifique que P é uma matriz estocástica regular e encontre o vetor de estado estacionário da cadeia de Markov associada. P = 1 / 4 2 / 3 3 / 4 1 / 3
No exercício 5, em cada parte, determine se P é uma matriz estocástica regular. P = 1 / 5 1 4 / 5 0
No exercício 3, use as Fórmulas (11) e (12) para calcular o vetor de estado x 4 de duas maneiras diferentes. P = 0,5 0,6 0,5 0,4 ;x 0 = 0,5 0,5
No exercício 4, use as Fórmulas (11) e (12) para calcular o vetor de estado x 4 de duas maneiras diferentes. P = 0 , 8 0 , 5 0 , 2 0 , 5 ;x 0 = 1 0
Considere um processo de Markov com matriz de transiçãoO que representa a entrada 0?