Identifique, esboce e exiba as coordenadas de um foco da cônica contida no plano dada pela equação
Passo 1
Calculando o :
Logo, nossa cônica pode ser uma hipérbole ou um par de retas concorrentes certo??
Pra eliminar o termo misto, temos que fazer uma rotação em um ângulo dado por
Como , o nosso vale .
Usando as relações de mudança de coordenada dadas por
Vamos ter o sistema
Passo 2
Beleza, a gente tem e em função de e . Agora a gente vai substituir isso lá na equação do enunciado demorou?
Racionalizando:
Opa agora bora passar o 2 pro outro lado multiplicando
Agora vamos completar quadrados
(Repara que a gente acrescentou e do mesmo lado da igualdade, por isso não precisamos “compensar” do outro lado)
Então temos
Boa, isso nos dá uma hipérbole trasladada com parâmetros e .
Os focos dela em são e então temos que um foco em é
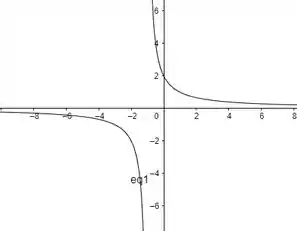
O esboço da cônica no plano é
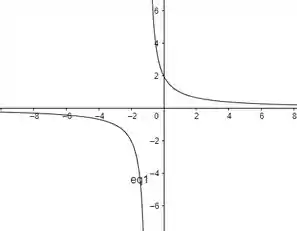
Resposta
Hipérbole.