UFPE – Geometria Analítica – 2018.1 – P3 – Questão 1
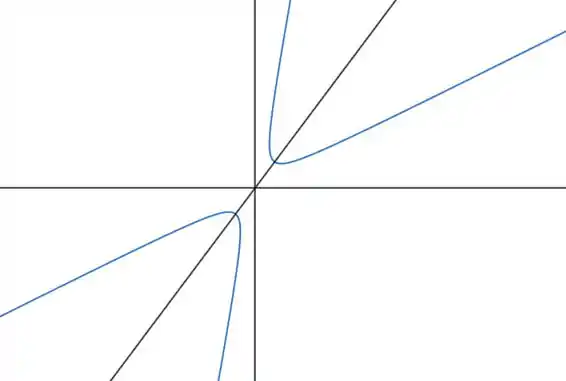
Encontre uma equação reduzida para a cônica e faça um esboço:
Passo 1
Iiih, galera, se apareceu esse termo é porque vamos ter que mexer com rotação de cônicas... Isso dá um trabalhinho, mas nada que a gente não seja capaz de resolver. Então bora lá! Vamos primeiro identificar os coeficientes, comparando com a cônica genérica:
O ângulo de rotação a gente vai tirar lá daquela fórmula:
E aí, os novos coeficientes da quádrica vão ser:
Passo 2
Vamos então chegar nesse seno que tá faltando.
Dividindo tudo por :
Passo 3
Substituindo:
Resolvendo, vamos obter:
Então, no novo sistema de coordenadas, vamos encontrar:
Essa cônica é uma hipérbole!
Resposta
Exercícios de Livros Relacionados
No exercício 7, verifique que P é uma matriz estocástica regular e encontre o vetor de estado estacionário da cadeia de Markov associada. P = 1 / 4 2 / 3 3 / 4 1 / 3
No exercício 5, em cada parte, determine se P é uma matriz estocástica regular. P = 1 / 5 1 4 / 5 0
No exercício 3, use as Fórmulas (11) e (12) para calcular o vetor de estado x 4 de duas maneiras diferentes. P = 0,5 0,6 0,5 0,4 ;x 0 = 0,5 0,5
No exercício 4, use as Fórmulas (11) e (12) para calcular o vetor de estado x 4 de duas maneiras diferentes. P = 0 , 8 0 , 5 0 , 2 0 , 5 ;x 0 = 1 0
Considere um processo de Markov com matriz de transiçãoO que representa a entrada 0?