Determine a equação reduzida e identifique a cônica dada pela equação abaixo. Esboce e indique as coordenadas dos focos no sistema de coordenadas .
Passo 1
Bom, vamo lá, a gente tem uma equação geral de uma cônica. Os coeficientes dela são
Como , essa cônica está rotacionada.
Além disso, como , ela não está transladada, ufaa!
Nesse caso, , então o ângulo não é e podemos demorar um pouco mais pra acharmos a equação reduzida, mas nada impossível viu?
Então bora lá ajustar essa belezinha pro sistema de coordenadas .
Passo 2
Precisamos descobrir pelo menos para descobrirmos os coeficientes e . Sabemos que
Passo 3
Achando a (é só inverter hehe)
Beleza, mas o que queremos é , temos por relação trigonométrica:
Agora que temos o podemos seguir em frente :D
Passo 4
ENCONTRANDO OS COEFICIENTES A’ E C’
Vamos descobrir os coeficientes e :
Somando as duas equações:
Substituindo na segunda equação:
Boaa, achamos os coeficientes e :)
Passo 5
ESCREVENDO A EQUAÇÃO REDUZIDA EM X’OY’
Como a equação não tem parte linear, agora vamos só reescrever a equação no sistema :
Dividindo tudo por :
Isso é a equação de uma elipse ao longo do eixo , onde , e .
Então os focos dessa elipse, no sistema são e .
ENCONTRANDO OS FOCOS NO SISTEMA XOY
Opa, mas queremos os focos no sistema !! E agora??
Para transformar as coordenadas do sistema em , temos a relação
Mas pra acharmos as coordenadas de e no sistema , precisamos de e !!
Passo 6
- Encontrar e
Tendo o sistema:
Podemos desenvolver a segunda equação assim:
Substituindo os valores que temos:
Então, nosso sistema fica assim
Passo 7
Somando as duas equações do sistema:
Substituindo isso na primeira equação:
Boaaa, agora podemos substituir naquela relação pra acharmos as coordenadas dos focos no sistema !!
Passo 8
- Substituindo na relação
Voltando à relação:
Vamos substituir as coordenadas dos focos e :
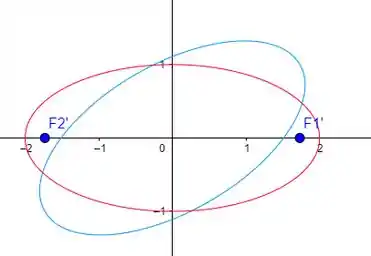
Então, as coordenadas dos focos no sistema são e .
Abaixo temos essa elipse nos dois sistemas de coordenadas
Resposta
e