Identifique e esboce a cônica dada pela equação
Passo 1
Temos um na nossa equação, então, a cônica está rotacionada certo?
Pra eliminar o termo misto, vamos fazer uma rotação, mas antes vamos encontrar o ângulo :
Como , o nosso vale .
Pelas relações de mudança de coordenada de para , vamos ter o sistema
Passo 2
Tendo e em função de e , agora a gente vai substituir isso lá na equação do enunciado demorou? (lembrando que como não temos e nem , não precisamos encontrar os coeficientes e )
Agora vamos dividir tudo por 4:
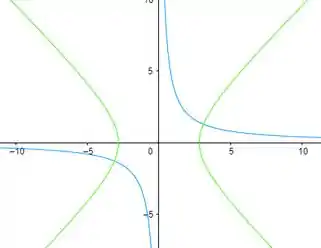
Boa, isso nos dá uma hipérbole com centro . Abaixo temos essa hipérbole esboçada no sistema (verde) e no sistema (azul)
Resposta
Hipérbole.
Exercícios de Livros Relacionados
No exercício 7, verifique que P é uma matriz estocástica regular e encontre o vetor de estado estacionário da cadeia de Markov associada. P = 1 / 4 2 / 3 3 / 4 1 / 3
No exercício 5, em cada parte, determine se P é uma matriz estocástica regular. P = 1 / 5 1 4 / 5 0
No exercício 3, use as Fórmulas (11) e (12) para calcular o vetor de estado x 4 de duas maneiras diferentes. P = 0,5 0,6 0,5 0,4 ;x 0 = 0,5 0,5
No exercício 4, use as Fórmulas (11) e (12) para calcular o vetor de estado x 4 de duas maneiras diferentes. P = 0 , 8 0 , 5 0 , 2 0 , 5 ;x 0 = 1 0
Considere um processo de Markov com matriz de transiçãoO que representa a entrada 0?