Identifique, esboce e determine as coordenadas de um foco (no sistema ) da cônica
Passo 1
Encontrando o ângulo de rotação
Antes de tudo, repara que a gente tem nessa cônica um termo misto , isso quer dizer o que?? Que vamos ter que fazer uma rotação hehe
Ta, mas em qual ângulo??
Vamos usar a relação:
A gente viu na teoria que a equação da cônica é escrita assim:
Então nesse caso, , e
Mas peraí!! A gente vai ter um 0 no denominador!!:
Pois é, isso quer dizer que a tangente desse ângulo não existe!!
Qual o ângulo que não tem tangente?? Issoo, o ângulo de !! Então sempre que , vamos ter:
Então vamos rotacionar nossa cônica em :D
Passo 2
Convertendo o sistema para
Vamos converter o sistema (equação do enunciado) no sistema (cônica rotacionada) usando a relação:
Sabendo que :
Beleza, temos e em função de e . Agora precisamos achar os coeficientes e da nossa cônica.
Passo 3
Encontrando os coeficientes e , análogos a e
Os novos coeficientes e vão ser dados pelo sistema:
Na nossa equação original, , então .
Além disso,
Então:
Somando as duas equações, temos
Substituindo na primeira linha:
Ou seja, não teremos o termo na nossa nova equação (pois ), enquanto o termo será multiplicado por 2.
Passo 4
Encontrando os termos lineares
Agora, vamos finalmente substituir as relações do sistema na parte linear da equação do enunciado.
Como assim na parte linear???
Isso quer dizer que vamos substituir apenas na parte que multiplica e :)
Fazendo a distributiva:
Ou seeeja, vamos substituir no lugar dos termos da equação original :D
Passo 5
Escrevendo a nova equação
Agora que temos os coeficientes , e o termo linear, vamos substituir na equação (lembrando que mantemos o termo independente ):
Passo 6
Identificando a cônica
Boaa, encontramos nossa cônica rotacionada, ela também pode ser escrita assim:
Isso dá pra gente a equação de uma parábola com vértice em e parâmetro .
O foco dessa parábola no sistema é .
Usando as equações do sistema pra transformar esse foco pro sistema :
Então no sistema .
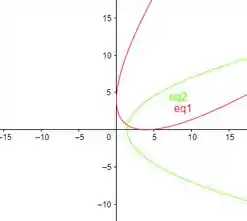
Abaixo temos o esboço da parábola original (vermelha) e rotacionada (verde).
Resposta
Parábola.
no sistema