Ache os pontos da reta que equidistam dos planos
Passo 1
Esse exercício é parecido com o anterior!! Mas, agora, queremos descobrir os pontos da reta que são equidistantes dos planos e . Para isso, se temos um ponto que pertence à reta , então:
Passo 2
Precisamos primeiro achar o ponto genérico ! Para isso, vamos primeiro colocar a equação que nos foi dada na forma simétrica para então podermos tirar os dados e escrever a equação vetorial da reta:
Então, e . Montando a equação vetorial temos:
Assim, conseguimos escrever :
Passo 3
Sabendo e sabendo que para e . Podemos colocar os valores na fórmula:
Igualando :
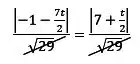
Elevando os dois membros ao quadrado:
Passo 4
Agora que sabemos que , podemos substituir em :
Então, os pontos equidistantes são:
Resposta
Exercícios de Livros Relacionados
Determine a equação do plano constituído de todos os pontos que são equidistantes dos pontos ( - 4,2 , 1 ) e ( 2 ,- 4,3 ) .
Determine a equação do plano constituído de todos os pontos que são equidistantes dos pontos (1,1,0) e (0,1,1).
Escreva as equações paramétricas da reta que passa pelo ponto P=( 1 ,2 ,3 ) e é perpendicular ao plano x-3 y+2 z=1 .
Determinar a distância da retar : {[[x = 3],[y = 4]]) d) ao plano pi : x + y - 12 = 0
Determinar a distância da retar : {[[x = 3],[y = 4]]) c) ao eixo dos z