Álgebra linear I, USP, P2, 2016, Questão 2
Seja a reta que passa pela origem e é paralela ao vetor . Se é um ponto do plano
Tal que a distância de à reta seja igual a 1, então:
Passo 1
Faaalaa, beleza?? Bora lá para mais uma questãozinha dessa prova, agora envolvendo distância entre ponto e reta.
Para entendermos o que iremos fazer, bora escrever a fórmula para calcular distância entre ponto e reta e depois vemos o que precisamos. Se tivermos um esqueminha do tipo:
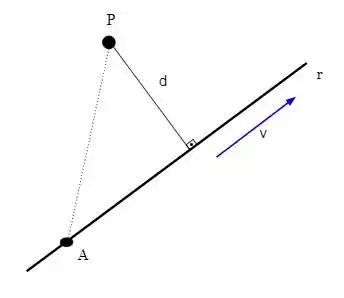
Temos que
Passo 2
Ou seja, para acharmos a distância entre um ponto e uma reta que tenha como vetor diretor basta pegarmos um ponto da reta e aplicar a fórmula.
Agora veja que pelo enunciado, temos que e , ou seja, temos que:
Ou seja:
Dai, vamos calcular :
E portanto, temos por laplace na primeira linha:
Ou seja, temos que
Passo 3
Agora, podemos notar que como , colocando na equação do plano temos que:
Ou ainda
Por isso, temos que:
E disso, tiramos que:
E colocando na fórmula:
Ou seja, temos que
Assim chegamos ao fim de outro probleminha, bora para o próximo?
Resposta
Letra E