Considere o plano e o ponto .
a) Escreva uma equação vetorial para a reta que passa pelo ponto e é perpendicular ao plano .
b) Determine o ponto que está mais próximo do ponto .
c) Determine o ponto que é simétrico de em relação ao plano . (Obs: é o ponto médio de .
Passo 1
a) Se a reta é perpendicular ao plano, o seu vetor diretor é um vetor normal do plano certo?
Para encontrarmos o vetor normal do plano , vamos fazer o produto vetorial entre seus vetores diretores, já que ele será perpendicular a esses dois vetores e, consequentemente, perpendicular ao plano. Pela equação do plano, a gente sabe que os seus vetores diretores são e , então o produto vetorial deles vai ser
Logo, o vetor , que é um vetor normal do plano, será um vetor diretor da reta.
Se a reta passa pelo ponto e tem como vetor diretor, sua equação vetorial é
Passo 2
b) Para que esse ponto pertencente ao plano seja o mais próximo possível do ponto , a distância entre eles deve estar em uma reta perpendicular ao plano, pois sabemos que a menor distância entre 2 pontos é uma linha reta.
Então o ponto vai ser a projeção do ponto no plano , ou seja, a intersecção da reta com o plano .
Vamos primeiro encontrar a equação geral do plano . Sabendo que é um vetor normal desse plano, temos que
Como o ponto pertence ao plano (como vemos na sua equação vetorial), vamos substituir para encontrar :
Logo, a equação geral do plano é
Passo 3
Um ponto genérico de é dado por (repare na equação encontrada no passo 1). Para encontrar a intersecção de com , vamos substituir esse ponto genérico de na equação geral de :
Logo, o ponto de que também passa por é aquele em que :
Uma figura do que fizemos até agora só pra ficar mais fácil de visualizar, sendo que o plano rosa é e a reta preta é :
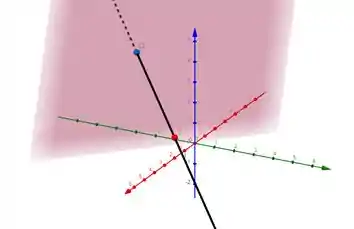
Passo 4
c) Se é o ponto médio de , o ponto vai ser tal que
Sabendo que (propriedades de vetores):
Isolando :
Substituindo os pontos e :
Resposta
a)
b)
c)