Considere as seguintes retas em
(b) Ache um vetor n ortogonal aos vetores e .
(c) Encontre a equação cartesiana do plano que é ortogonal ao vetor n e contém o ponto de . Determine se a reta está contida no plano .
(d) Determine a distância d entre o plano e a reta .
(e) Determine explicitamente um ponto B do plano tal que a distância entre B e seja d.
Passo 1
(b) Se queremos achar um vetor ortogonal a e basta fazer o produto vetorial entre eles:
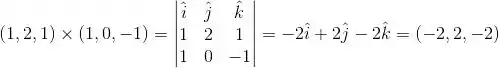
Ou seja, qualquer vetor paralelo a é ortogonal a esses dois vetores.
Podemos escolher por exemplo:
Passo 2
(c) A equação cartesiana do plano é da forma:
Onde (a,b,c) são as coordenadas de um vetor normal ao plano.
Como o plano tem que ser ortogonal ao vetor achado na letra (b), então a equação fica:
Esse plano também deve conter o ponto .
Substituindo as coordenadas do ponto nessa expressão:
Logo, a equação do plano é:
Agora precisamos dizer se a reta está contida no plano .
Bom, os pontos da reta são da forma:
Substituindo x,y e z na equação do plano por essas coordenadas, vamos obter:
Ou seja, todos os pontos de satisfazem a equação do plano .
Então todos os pontos da reta pertencem ao plano e a reta está contida no plano.
Passo 3
(d) Agora precisamos achar a distância entre e , mas antes vamos ver a posição relativa entre eles.
O vetor diretor da reta é e o vetor normal do plano é (-1,1,-1).
Fazendo o produto interno entre eles:
Ou seja, os dois são ortogonais entre si.
Logo, a reta é paralela ao plano.
Isso significa que todos os pontos da reta estão à mesma distância do plano.
Então pra achar a distância entre eles, eu posso escolher um ponto qualquer da reta e calcular a distância desse ponto ao plano através da formulazinha:
Vamos escolher o ponto de .
Substituindo na fórmula:
Passo 4
(e) Vimos, no item (d), que qualquer ponto da reta está a mesma distância do plano, e usamos o ponto para achar essa distância .
Agora precisamos achar o ponto S no plano que está a essa distância desse ponto R.
É mais ou menos assim:
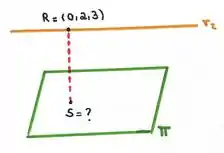
Vamos considerar a reta s de vetor diretor igual ao vetor normal do plano e que contém o ponto
Sua equação é:
Nesse caso, o ponto S é a interseção dessa reta s com o plano
Os pontos da reta s satisfazem:
Substituindo esses valores na equação do plano
Logo, a interseção do plano com a reta s vai ter coordenadas:
Esse ponto é justamente o ponto S que estávamos buscando!
Portanto:
Resposta
(b) (ou qualquer múltiplo escalar desse vetor)
(c)
A reta está contida no plano
(d)
(e)