Seja o plano que passa pelo ponto e contém a reta
Se é a reta dada pela interseção de com o plano , então um vetor diretor para é:
- ;
- ;
- ;
- ;
- .
Passo 1
E aí, meu povo? Como vocês estão? Nossa questão tá pedindo um vetor diretor para a reta dada pela interseção do plano com o plano . Beleza... mas a gente não sabe quem é o tal plano ainda né hahaha. Primeiramente, vamos relembrar qual é a equação geral de um plano:
Nessa equação são as coordenadas de algum ponto que saibamos pertencer ao plano e são as coordenadas de um vetor normal ao nosso plano.
Show de bola então! Porque se tivermos a equação do nosso plano , só vamos precisar fazer nela para encontrarmos a reta pedida.
Beleza, mas qual vai ser a nossa estratégia para descobrir aqueles termos então? Que bom que você perguntou! Lembra do produto vetorial? Se conhecermos dois vetores que pertençam ao plano e fizermos o produto vetorial, obtemos um novo vetor perpendicular a eles e, por consequência, normal ao plano.
Por sorte, nem vamos precisar calcular , já que no enunciado mesmo vem dizendo que o plano passa pelo ponto . Só precisamos mesmo descobrir os tais termos . Show? Vamos lá então.
Passo 2
Só pra facilitar nossa comunicação, vou estabelecer algumas nomenclaturas, tá bom? Nada demais, fica tranquilo! Haha
Vou chamar o ponto pelo qual o plano passa de :
Além disso, o enunciado nos dá também uma reta que pertence ao plano . Vou chamar o ponto pelo qual essa reta passa de e o seu vetor diretor de :
Com essas nomenclaturas estabelecidas, temos a seguinte situação, ilustrada na figura abaixo:
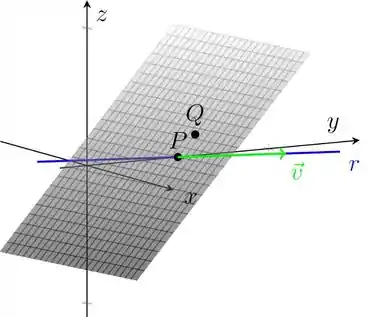
Como a reta já pertence ao nosso plano, isso vale também para o seu vetor diretor , certo? Então basta encontrarmos mais um vetor pertencente a .
A nossa figura já nos sugere algo bem interessante: nós conhecemos o ponto da reta e o ponto . Se nós criarmos um vetor ligando esses dois pontos, resolvemos nosso problema! Isso está ilustrado com o vetor em vermelho na figura abaixo.
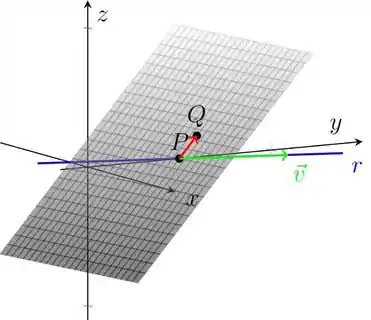
Temos então:
Show de bola! Conforme a estratégia que mencionamos lá em cima, basta a gente agora fazer o produto vetorial entre e :
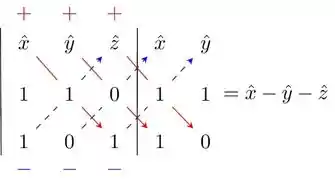
Logo, nosso vetor normal é:
Substituindo e na equação do plano, temos:
Rearranjando:
Passo 3
Belezinha! Como agora já temos a equação do plano, falta nosso passo final, fazer para encontrarmos a reta que vem da interseção do plano com :
Temos então:
Para encontrar um vetor diretor, vamos parametrizar a reta , tomando . Então, da equação de , temos:
Logo:
Um vetor diretor para é então:
Bora pra próxima questão? 😊
Resposta
(e) .