Prova P1 – 2019.1– USP – Probabilidades – Teste 9
Considere três eventos A, B e C. Considere:
- ;
São verdadeiras apenas as afirmações:
- (a) e (b) e (c);
- (a) e (c);
- (b) e (c);
- (b);
- (a) e (b).
Passo 1
Eaeeeeee, belezinha??
Spoiler!!! Essa questão aqui é legal só porque você quase nem vai ler, vamos representar as afirmativas em imagens e depois observar a lógica pra decidir quais são verdadeiras ou falsas!
Na primeira afirmação, temos que , ou seja:
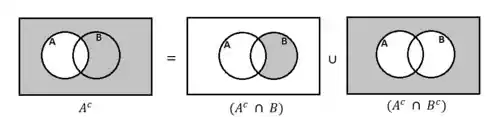
Percebe-se que a soma das áreas hachuradas correspondem à igualdade. Portanto, a primeira afirmação está CORRETA!!
Passo 2
Na segunda afirmação, temos que , ou seja:
Dessa forma, também percebemos que a soma das áreas hachuradas à esquerda da igualdade corresponde com o lado direito. Assim, a segunda afirmação também está CORRETA!!
Passo 3
Na terceira afirmação, temos que , ou seja:
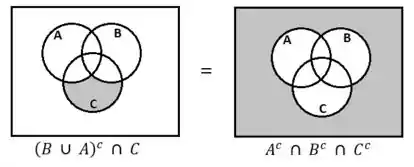
Percebemos que essa igualdade não é válida pois não há correspondência entre os conjuntos. Assim, temos que a alternativa correta é a letra e).
Entendeu direitinho??? Valeeeu, até a próxima!
Resposta
e) (a) e (b)