Teste 1 Sejameventos com as seguintes probabilidades . Considere:

São verdadeiras apenas as afirmações:

Vamos começar pela primeira afirmação, letra a)

A letra a) nos diz que , mas será que é verdade?

O que podemos dizer sobre

Podemos reescrever como

Com isso temos que

Chegamos em algo próximo a afirmação de que , mas infelizmente não sabemos que é . Mas podemos obter uma estimativa para . Para isso vamos utilizar diagrama de Venn.

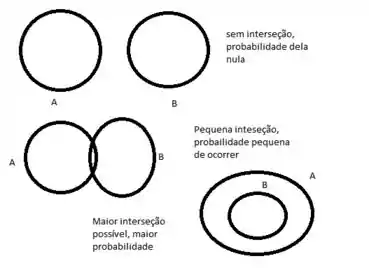
Então podemos observar que a maior probabilidade possível para a interseção será ocorrerá quando . ou seja quando fazendo com que .

Pelo argumento acima conseguimos observar que então vamos pegar o maior valor possível para a interseção, isto é

Então teríamos que

(substituindo a intersecção pelo maior valor possível)

Como todos os demais valores possíveis de são menores que Chegamos à conclusão que

A primeira afirmação é verdadeira!! Vamos checar a terceira afirmação, pois já fizemos algumas observações sobre afirmação

A afirmação c) diz que . Como vimos no passo anterior, sabemos que é o máximo para essa probabilidade, mas será que é o mínimo para essa probabilidade? Vamos descobrir

Sabemos que , logo

Opaaaa tem alguma coisa estranha, pois sabemos que a probabilidade de um evento não pode ser maior que 1. Isso implica que a intersecção entre NÃO pode ser vazia.

Sendo assim, como

Temos que

Logo obtemos que

Então a letra c) não é verdadeira, pois não contem todos os possíveis valores para a intersecção.

Agora só precisamos verificar a firmação b). Queremos saber se é verdade que

Vamos retorna ao nosso amigo, diagrama de Venn, para visualizar melhor quem é

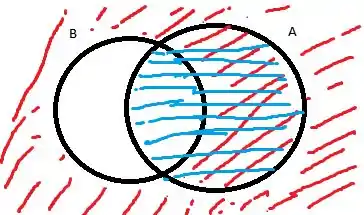
Em azul temos o evento e em vermelho , então a interseção será a região pintada de azul e vermelho simultaneamente.

Ao olhar o diagrama fica mais fácil de ver que . Calculamos a probabilidade de e subtraímos da interseção.

Usando o resultado que obtemos no passo anterior, sabemos que e também temos que

Então

(multiplicando por -1)

(somando P(A) nas desigualdades)