O tempo de travessia de uma balsa é uma variável aleatória que assume os valores , e minutos com probabilidades iguais. Carlos pega esta balsa diariamente para ir ao trabalho. Entretando, ele não consegue pegar a conexão com o ônibus da firma se o tempo gasto com a travessia for . Não pegando o ônibus ele consegue um taxi com probabilidade , e, neste caso, chega a tempo no serviço. Não conseguindo um taxi ele vai a pé e chega atrasado. Sua firma tem a política de tolerar no máximo de atrasos por ano.
- Calcule a probabilidade de que, num dia normal de trabalho, Carlos chegue atrasado no serviço.
Passo 1
Vamos anotar melhor esses dados...
A travessia da balsa pode ocorrer em três tempos diferentes:
Cada uma delas tem probabilidade igual de acontecer... isso significa que a balsa demorar ou minutos tem a mesma chance que é:
Show?
Mas tem um porém... se ele pega a balsa de ou minutos, ele consegue pegar o ônibus e chegar em tempo pro trabalho. Mas pegando a de minutos, ele perde o ônibus.
Mas nem tudo está perdido...
Perdendo o ônibus, ele tem chance de de pegar um táxi e ainda chegar na hora.
Passo 2
Vamos organizar isso numa árvore de probabilidade? Acho que vai ficar bacana!
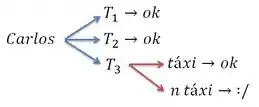
Cada seta azul tem o valor de e cada seta vermelha vale , certo?
E essa carinha triste aí simboliza a situação em que ele chega atrasado.
Passo 3
(a)
Pra calcular a prob. dele chegar atrasado é só seguir as setas levando até a carinha triste.
Precisam acontecer duas coisas:
- Pegar a balsa ;
- Não conseguir pegar o táxi.
Então: