Uma central de energia às margens de um rio, como na figura abaixo, deve eliminar de calor perdido para o rio. As condições do rio a montante são e . O rio tem de largura e de profundidade. Se as perdas de calor para a atmosfera e para o solo são desprezíveis, calcule as condições do rio a jusante .
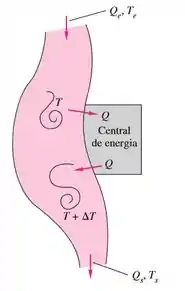
Passo 1
Vamos começar escolhendo nosso volume de controle. Nesse caso é interessante que a central de energia esteja dentro do nosso volume de controle.
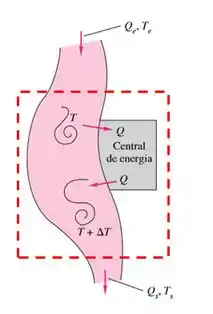
Agora podemos montar a equação de energia, nesse caso temos apenas calor sendo dissipado. Se lembrarmos da equação de calor é , como estamos sempre falando de fluxo de calor:
O fluxo de massa é igual e podemos abrir ele como .
Como o fluxo de massa são iguais, temos que a vazão de entrada é igual a vazão de saída.
Em uma tabela de vemos que o da água é