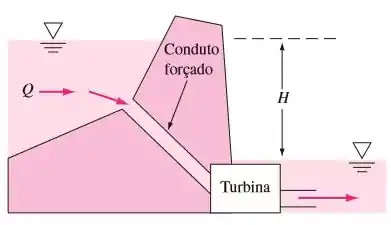
Considere a turbina extraindo energia através de um conduto forçado em uma barragem, como na figura abaixo. Para escoamento turbulento em dutos, a perda de carga por atrito é aproximadamente , em que a constante depende das dimensões do conduto forçado e das propriedades da água. Mostre que, para uma dada geometria de conduto forçado e vazão variável do rio, a máxima potência possível da turbina nesse caso é e ocorre quando a vazão é .
Passo 1
Nessas questões, temos que primeiro escolher as superfícies que vamos usar para estudar a energia.
Iremos analisar a superfície que é a superfície do maior reservatório e a superfície que é a superfície do líquido após passar pela turbina. Isso vai nos permitir fazer algumas simplificações.
Lembra que quando tratamos de reservatórios vamos considerá-los tão grandes que a altura da superfície não varia? Assim .
Vamos colocar nosso eixo na superfície . Assim e .
E ambas superfícies estão expostas a pressão atmosféricas.
Então escrevendo a equação de energia temos:
Passo 2
E retirando aquele termo que tá repetido dos dois lados:
Isolamos o porque, afinal, é a potência da turbina que vamos querer estudar. E a potência da turbina está correlacionada com o , que é a carga consumida pela turbina.
O enunciado nos definiu que .
A potência da turbina a gente viu lá na teoria que é:
Então:
Passo 3
Tudo muito lindo, mas e agora?
O problema fala de pressão máxima, certo? Como descobrimos o máximo de uma função??
Sim, temos que derivar e igualar a zero. Assim:
Então descobrimos que a turbina vai ter potência máxima quando .
E nesse caso a potência será de:
Resposta
Ei, a resposta está no passo a passo :)