Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação da Energia e Bernoulli

Ver Teoria
Exercício 111234567891012131415

Enunciado

UPS – Mecânica dos fluidos – 2018.2 – P2. 3.1

Óleo SAE 10 a 20°C ( ρ o = 870   k g / m ³ , μ = 0,104   P a . s ) escoa no interior do tubo vertical liso de 30 mm de diâmetro interno mostrado na figura. O desnível do manômetro de mercúrio ( ρ H g = 13600   k g / m ³ ) é de 420 mm, conforme mostrado na figura. A aceleração da gravidade é de 9,8 m/s². Determine:

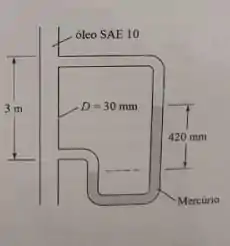
  1. O sentindo do escoamento

Passo 1

Para resolver esse problema vamos precisar calcular a perda de carga h L , se esse valor for maior que zero, temos que o escoamento ocorre de baixo para cima, caso contrário, de cima para baixo.

A equação de energia aplicada no tubo reto é:

p 1 γ + α 1 V 1 2 2 g + z 1 - p 2 γ + α 2 V 2 2 2 g + z 2 = h L

Bem, considerando que o tubo tem área transversal constante, V 1 = V 2 , logo:

p 1 - p 2 γ + z 1 - z 2 = h L

Passo 2

Aplicando a lei de Stevin no manômetro para achar a diferença de pressão p 1 - p 2 , temos que:

p 1 - p 2 = - d 1 γ + 0,42 γ H g + d 2 γ

p 1 - p 2 = 3 - 0,42 γ + 0,4 γ H g

p 1 - p 2 = 9,8 2,58 × 870 + 0,42 × 13600 = 77975   P a

Substituindo esse valor na equação de energia, encontramos que:

h L = 77975 870 × 9,8 - 3 = 6,146

Como h L > 0 , temos o escoamento de baixo para cima

Resposta

Como h L > 0 , temos o escoamento de baixo para cima

Exercícios de Livros Relacionados

Reanalise o problema 3.54 para estimar a leitura no manômetro h através da equação de Bernoulli. Para h = 58 cm do problema 3.54, qual é a perda de carga?
Os tanques A e D são de grande dimensões e o tanque C é de pequenas dimensões, mas o nível (4) permanece constante. A bomba B, que tem η B = 80 % , recebe 11 kW do motor elétrico e tem carga manométri
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se o fluido manométrico tem densidade de 1,6 e se h = 66c m , com o atrito desprezado, qual é a velocidade média na seção 2? (a)
A água escoa a uma vazão de 20L / s através de um tubo horizontal cujo diâmetro de uma válvula do tubo é medida como 2k P a . Determine a perda de carga irreversível da válvula, e a potência de bombea
Uma bomba de 7hp (eixo) é usada para elevar a água até 15m de altura. Se a eficiência mecânica da bomba for de 82 % , determine a vazão de volume máxima da água.