A bomba da figura abaixo cria um jato d’água a , orientado para atingir uma distância horizontal máxima. As perdas por atrito do sistema são de . O jato pode ser aproximado pela trajetória de partículas sem atrito. Que potência a bomba deve entregar à água?
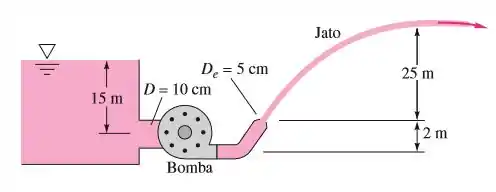
Passo 1
Pra resolver esse exercício, precisamos da equação de energia.
E para aplicar essa equação, vamos ter que definir o volume de controle, com limites onde temos bastante informações.
Então vamos posicionar o nosso ponto 1 de controle na superfície do reservatório e o ponto 2 na saída do tubo, no início do lançamento.
No ponto 1, consideramos:
Já no ponto 2, vamos ter:
O nosso , porque colocamos a origem do nosso eixo z nessa altura ok?
E já sacamos que vamos ter que determinar aquela velocidade ali que tá faltando.
Passo 2
O problema aqui é você sacar que pra alcançar a distância horizontal máxima a inclinação do lançamento deve ser . Isso não é óbvio, mas como você está fazendo esse exercício, já vai saber na próxima vez que precisar disso.
E com essa informação, vamos usar Torricelli para saber a velocidade do jato de água no inicio do lançamento.
Na altura máxima a velocidade em é zero (já que ele para de subir e começa a descer), assim, temos que:
Aí a gente tem a componente da velocidade no eixo z, que é igual a velocidade total vezes o sem de , que a gente definiu como 45°. E a aceleração no eixo z é a gravidade mesmo.
Passo 3
Agora que temos a velocidade em 2, podemos voltar para a equação da energia.
Que com o que a gente tem até agora:
Onde , as perdas por atrito.
A gente pode, então, cortar aqueles termos iguais e reorganizar um pouco a galera:
Pra achar:
Como queremos a potência da bomba: