Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação da Energia e Bernoulli

Ver Teoria
Exercício 123456789101112131415

Enunciado

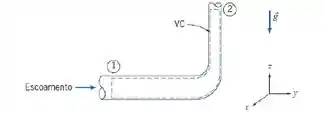
(Adaptada) Medidas foram feitas para a configuração de escoamento de água mostrada na figura. Na entrada, seção 1, a pressão é 70kPa (manométrica), a velocidade média é 1,75 m/s e a elevação é 2,25 m. Na saída, seção 2, a pressão, a velocidade média e a elevação são, respectivamente, 45 kPa (manométrica), 3,5 m/s e 3 m, respectivamente. Calcule a perda de carga em metros.

Passo 1

Primeiro, vamos anotar direitinho quem é quem. Na entrada (seção 1), temos:

p 1 = 70   k P a =   70 × 10 3 P a v 1 = 1,75   m / s z 1 = 2,25   m

Já na saída (seção 2), temos:

p 2 = 45   k P a =   45 × 10 3 P a v 2 = 3,5   m / s z 2 = 3   m

Opa! Então o enunciado nos deu todos os dados de pressão, velocidade e elevação. Com a equação da energia, vamos conseguir calcular a perda de carga que foi pedida.

Passo 2

A equação da energia é:

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h p e r d a s - h b o m b a + h t u r b i n a

Como não há bomba nem turbina no nosso volume de controle (que já foi definido na figura do enunciado), então h b o m b a = 0 e h t u r b i n a = 0 . Atualizando a equação da energia:

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h p e r d a s

Vamos substituir os valores separados no Passo 1 e calcular a perda de carga h p e r d a s

70 × 10 3 ρ g + 1,75 2 2 g + 2,25 = 45 × 10 3 ρ g + 3,5 2 2 g + 3 + h p e r d a s

70 × 10 3 - 45 × 10 3 ρ g + 1,75 2 - 3,5 2 2 g + 2,25 - 3 = h p e r d a s

Lembrando que o fluido é a água ρ = 1000   k g / m 3

h p e r d a s = 25 × 10 3 10 3 × 9,8 + 1,75 2 - 3,5 2 2 × 9,8 - 0,75

h p e r d a s = 2,551 - 0,469 - 0,75

h p e r d a s = 1,332   m

Encontramos a perda de carga! :D

Resposta

h p e r d a s = 1,332   m

Exercícios de Livros Relacionados

Reanalise o problema 3.54 para estimar a leitura no manômetro h através da equação de Bernoulli. Para h = 58 cm do problema 3.54, qual é a perda de carga?
Os tanques A e D são de grande dimensões e o tanque C é de pequenas dimensões, mas o nível (4) permanece constante. A bomba B, que tem η B = 80 % , recebe 11 kW do motor elétrico e tem carga manométri
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se o fluido manométrico tem densidade de 1,6 e se h = 66c m , com o atrito desprezado, qual é a velocidade média na seção 2? (a)
A água escoa a uma vazão de 20L / s através de um tubo horizontal cujo diâmetro de uma válvula do tubo é medida como 2k P a . Determine a perda de carga irreversível da válvula, e a potência de bombea
Uma bomba de 7hp (eixo) é usada para elevar a água até 15m de altura. Se a eficiência mecânica da bomba for de 82 % , determine a vazão de volume máxima da água.