Um jato de álcool atinge a placa vertical da figura abaixo. Uma força é necessária para manter a placa estacionária. Considerando que não há perdas no bocal, calcule o fluxo de massa de álcool e a pressão absoluta na seção .
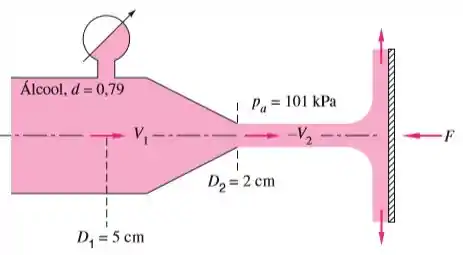
Passo 1
Fazendo a analise de momento linear na direção , chegamos em: (esse resultado é melhor explicado em um exercício da teoria de momento linear).
Como o enunciado falou , temos que a velocidade será:
Tendo a velocidade em , conseguimos calcular a vazão mássica.
Passo 2
Agora vamos usar a conservação se massa para encontrar
Agora por Bernoulli sem perdas pois nesse caso não há nenhuma perda, podemos escrever a equação:
Como o escoamento não muda de altura temos que
Podemos cortar e multiplicar por
Resposta
Exercícios de Livros Relacionados
Reanalise o problema 3.54 para estimar a leitura no manômetro h através da equação de Bernoulli. Para h = 58 cm do problema 3.54, qual é a perda de carga?
Os tanques A e D são de grande dimensões e o tanque C é de pequenas dimensões, mas o nível (4) permanece constante. A bomba B, que tem η B = 80 % , recebe 11 kW do motor elétrico e tem carga manométri
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se o fluido manométrico tem densidade de 1,6 e se h = 66c m , com o atrito desprezado, qual é a velocidade média na seção 2? (a)
A água escoa a uma vazão de 20L / s através de um tubo horizontal cujo diâmetro de uma válvula do tubo é medida como 2k P a . Determine a perda de carga irreversível da válvula, e a potência de bombea
Uma bomba de 7hp (eixo) é usada para elevar a água até 15m de altura. Se a eficiência mecânica da bomba for de 82 % , determine a vazão de volume máxima da água.