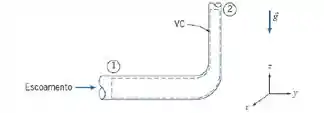
Para a configuração de escoamento da figura, é sabido que a perda de carga é 1 m. Da entrada para a saída, a queda de pressão é 50 kPa, a velocidade dobra da entrada para a saída, e o aumento de elevação é de 2 m. Calcule a velocidade de entrada da água.
Passo 1
Dessa vez o enunciado deu as variáveis da equação da energia de uma forma um pouquinho diferente. O primeiro passo é escrever quem são essas variáveis.
Pela figura, vemos que a seção 1 corresponde à entrada e a seção 2 à saída.
O é negativo pois houve uma queda de pressão, ou seja, . Logo, podemos reescrever essa relação:
Agora sim, vamos para a equação da energia!
Passo 2
A equação da energia é:
Lembrando que, como não tem bomba nem turbina no volume de controle, então e . Logo, a equação da energia fica:
E agora, reorganizando os termos para podermos substituir o que encontramos pelo enunciado:
Substituindo:
Logo, a velocidade de entrada é 3,7 m/s