UPS – Mecânica dos fluidos – 2018.2 – P2. 2.1
Dois reservatórias de água abertos para a atmosfera são conectados por uma tubulação de mesmo material e diâmetro constante de 50 mm e uma máquina hidráulica M, garantindo-se um escoamento permanente, conforme esquematizado na figura abaixo. Os seguintes dados são fornecidos para essa instalação: , , , , , e . Pede-se:
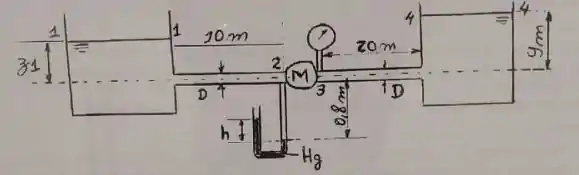
- Mostrar por meio de cálculo o sentido do escoamento. Justificar o valor do coeficiente de energia cinética adotado
Passo 1
Bem, como a gente pode verificar o sentindo do escoamento? Existem praticamente duas formas de saber isso, sabe-se que o escoamento escoa do local de maior pressão para o ponto de menor pressão OU local com maior altura manométrica para o de menor valor.
Nesse caso, o problema nos deu condições de calcular as alturas manométricas, então a gente pode calcular as alturas manométricas no ponto 3 e 4.
Passo 2
A fórmula para calcular isso é:
Onde
O valor de depende do tipo de escoamento, se ele for turbulento esse valor é unitário. Então, vamos calcular o valor de Re e verificar isso!!
Mas como podemos calcular a velocidade? Bem, foi dado pra gente a vazão volumétrica e sabemos o diâmetro do tubo, logo, podemos relacionar
Mas a vazão foi dada em L/s, vamos passar isso pro SI, ou seja, para m³/s.
Então, a velocidade pode ser calculada tal que:
Então, podemos considerar
Passo 3
Agora que temos a velocidade de escoamento, podemos calcular as alturas manométricas no ponto 3 e 4.
No enunciado foi dado pra gente a e além disso .
Para o ponto 4, temos:
Na superfície do tanque, temos que e , certo? Mas na equação de altura manométrica, onde tem a pressão é como se já estivéssemos descontando a pressão atmosférica, ou seja,.
Como , o sentindo do escoamento é de 3 para 4.