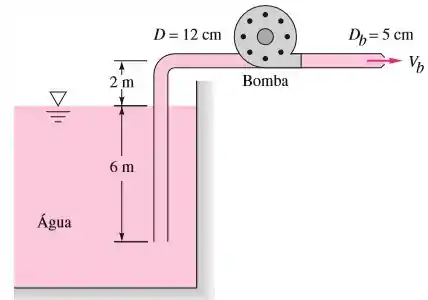
Quando a bomba da figura abaixo bombeia de água a do reservatório, a perda de carga total por atrito é de . O escoamento descarrega através de um bocal para a atmosfera. Calcule a potência da bomba em entregue para a água.
Passo 1
Vamos começar definindo as superfícies de analise de energia.
Assim, temos superfície na superfície do reservatório e uma superfície na saída do fluido.
Precisamos descobrir quanto vale e para isso vamos usar o fato do enunciado nos ter fornecido a vazão da bomba. Como o fluido é a água o fluido é incompressível e por isso podemos falar que a vazão que a bomba impõe é igual à vazão de saída.
E a velocidade com que o reservatório desce?? Se liga nessa dica, ela vai ser muito usada.
Em questões de reservatório se considera que o volume de água é tão mais tão grande que sua altura não muda, assim .
Agora vamos aplicar a equação de conservação de energia. Como a vazão mássica é igual, podemos escrever o sistema como vimos na teoria:
Agora vamos considera nosso eixo na superfície , assim
A pressão em é a pressão atmosférica e a pressão em também é .
é a perda por fricção ou atrito, assim o enunciado nos disse que vale
Então ficamos com a seguinte equação
Mas queremos a potencia da bomba, assim temos que lembrar que a potencia de uma bomba é dada por: