Caracterize analiticamente, provando suas conclusões passo-a-passo, o fator de forma entre a superfície 1 e 2, escrevendo esse fator de forma em função de fatores elementares de forma que esses possam ser encontrados em figuras ou tabelas.
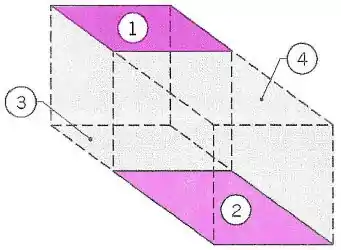
Determine também qual a transferência de calor entre 1 e 2, assumindo que em 1 a temperatura seja de e em 2 a temperatura seja de , sabendo que ambas as superfícies são aço inoxidável, típico, polido. Sabendo também que o meio interno a essa superfície é composto por vácuo.
Passo 1
Usando a regra da superposição, podemos dizer que:
Passo 2
Os fatores de forma , e podem ser encontrados pelo gráfico abaixo:
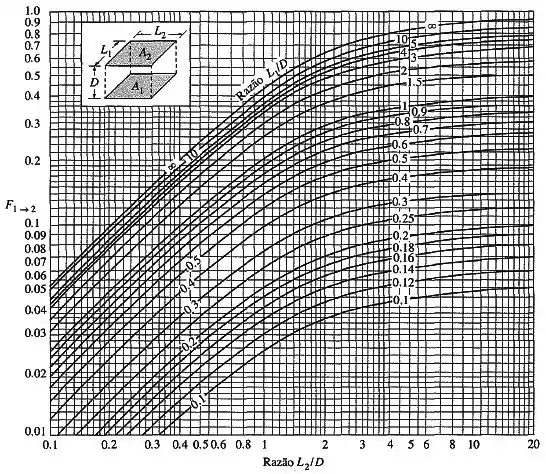
Passo 3
Para calcular o fator de forma , ainda precisamos lidar com o fator de forma .
Pela regra da simetria:
E, pela regra da reciprocidade:
Onde . Dessa forma:
Logo:
Substituindo na expressão que encontramos no Passo 1:
Agora é só uma questão de arrumar a bagunça:
![]()
Passo 4
Como o problema não nos deu a emissividade das superfíciesA transferência de calor será dada por:
Para calcular o fator de forma , temos que, considerando cada superfície quadrada e que a distância entre as superfícies é igual ao lado de cada uma delas:
Assim:
Passo 5
A taxa de transferência de calor será:
De acordo com a tabela A.11 do Incropera, para aços inoxidáveis, típicos e polidos:
Dessa forma, considerando :
Como não temos o valor de :
O sinal negativo se dá pelo fato de que, como a superfície 1 possui uma temperatura menor que a superfície 2, o calor na verdade flui de 2 para 1. Logo:
![]()