(Adaptado) Um anel com de raio interno e de raio externo é uma peça de aquecimento por radiação de um plano em formato de disco de de raio paralelo ao anel a uma distância de .
Toda uma região que fecha o sistema (forma uma cavidade fechada) é formada de um material que isola o sistema, ou seja, por uma superfície reirradiante.
Sabendo que o anel está a e emite radiação como um corpo negro e que o disco inferior está a e é um corpo cinza e difuso que possui uma emissividade de , determine qual o fluxo de calor radiante entre o disco e o anel.
Passo 1
A taxa de transferência de calor entre as duas superfícies é dada por:
Graficamente, a ideia é essa:
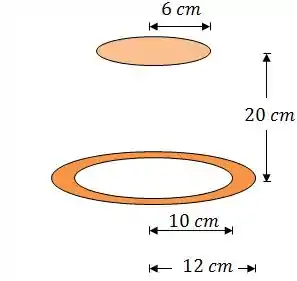
Da equação da taxa de transferência de calor, o único termo que nos resta calcular é o fator de forma.
Passo 2
Pra calcular o fator de forma, vamos criar uma superfície imaginária da seguinte forma:
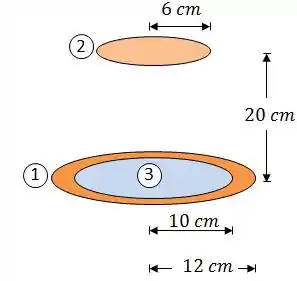
De forma que, pela regra da superposição:
Os fatores de forma e podem ser calculados a partir do gráfico abaixo.
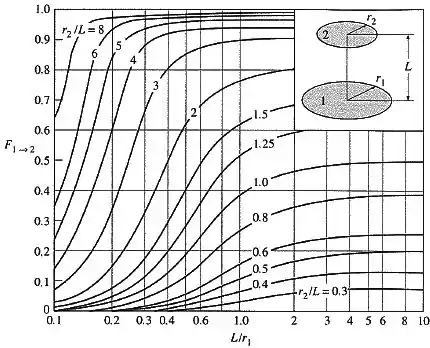
Onde, para :
E, para :
Assim:
Dessa forma, o fator de forma será:
Passo 3
A taxa de transferência de calor será:
Como o anel emite radiação como corpo negro , podemos reescrever a equação acima como:
Substituindo os valores:
![]()