No fundo de uma grande câmara de vácuo cujas paredes estão a , um painel negro com de diâmetro é mantido a .
Para reduzir o calor ganho nesse painel, uma barreira de radiação com o mesmo diâmetro e uma emissividade de é colocada muito próximo ao painel.
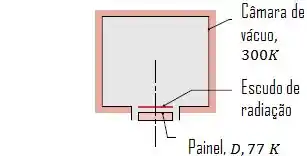
Calcule o ganho líquido de calor no painel.
Passo 1
A taxa de transferência de calor será dada por:
Contabilizando todas as resistências à radiação do sistema, temos o seguinte:
Passo 2
Como ou , a primeira resistência à radiação será aproximadamente nula. Além disso, como a placa é uma superfície negra, , zerando a última resistência à radiação.
Dessa forma:
Onde:
Logo:
Arrumando a bagunça:
Passo 3
Assim, a taxa de transferência de calor será dada por:
Onde .
Dessa forma:
Resposta
Exercícios de Livros Relacionados
97 – Irradiação da superfície da terra da atmosfera exibe uma variação espectral forte, principalmente associado com a janela atmosférica na Seção 12.9.2.A) Para uma faixa 0 ≤ λ ≤ 8 μm a emissividade
91 – A radiação solar incidente na superfície da Terra pode ser dividido em componentes direto e difusivo no Problema 12.90. Considere condições para um dia na qual a intensidade da radiação solar dir
A superfície exposta de um amplificador de potência de um receptor utilizado em um satélite terrestre, com área de 130m m por 130m m , tem um revestimento opaco, cinza e difuso, com uma emissividade d
Um disco metálico circular, com diâmetro de 0,4m , é firmemente posicionado contra o solo em uma região estéril, horizontal, onde a terra está a uma temperatura de 280K . A temperatura do céu efetiva
A asa de alumínio oxidado de um avião tem um comprimento de corda deL c =4m e uma emissividade hemisférica espectral caracterizada pela distribuição mostrada na figura.(a) Considere condições nas quai