Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Radiação entre Superfícies

Ver Teoria
Exercício 131234567891011121415

Enunciado

(Adaptado) Uma sala de 2   m e t r o s de lado contém duas placas identificadas como 1 e 2 na figura abaixo.

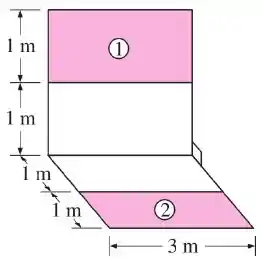
As demais faces da sala são reirradiantes. Sabendo que a placa 1 está a 2000   K e emite radiação como um corpo negro e que a placa 2 está a 200   K e é um corpo cinza e difuso que possui uma emissividade de 0,4 , determine:

( a ) provando matematicamente, quais os fatores de forma associados ao sistema.

( b ) o fluxo de calor radiante entre as placas 1 e 2.

Passo 1

( a ) Determine, quais os fatores de forma associados ao sistema.

A ideia aqui é a seguinte: vamos completar a parede da seguinte forma.

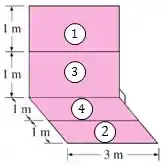
Onde queremos determinar os fatores de forma F 1 → 2 e F 2 → 1 . Os dois estão relacionados pela regra da reciprocidade, dada por:

A 1 .   F 1 → 2 = A 2 .   F 2 → 1

Como A 1 = A 2 :

F 1 → 2 = F 2 → 1

Passo 2

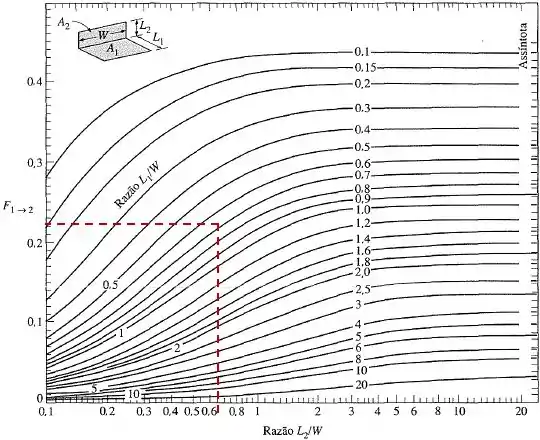
Utilizando os gráficos, podemos determinar os fatores de forma F 1,3 → 2,4 e F 3 → 4 .

Dessa forma, para o primeiro caso, teremos:

L 1,3 W = 2 3 = 0,67

L 2,4 W = 2 3 = 0,67

F 1,3 → 2,4 = 0,22

Para o segundo caso:

L 3 W = 1 3 = 0,33

L 4 W = 1 3 = 0,33

F 3 → 4 = 0,25

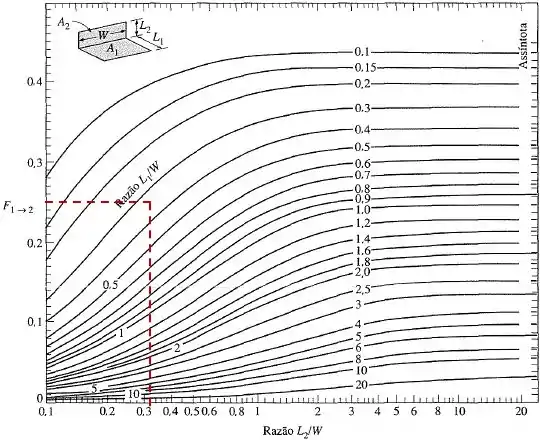
Passo 3

Através da regra da superposição, temos que:

A 1 + A 3 F 1,3 → 2,4 = A 1 F 1 → 2,4 + A 3 F 3 → 2,4

A 1 + A 3 F 1,3 → 2,4 = A 1 . F 1 → 2 + A 1 . F 1 → 4 + A 3 . F 3 → 2 + A 3 . F 3 → 4

Dessa equação, precisamos dos fatores de forma F 3 → 2 e F 1 → 4 . No entanto, devido à regra da simetria, podemos afirmar que:

F 3 → 2 = F 1 → 4

Assim, teremos o seguinte:

F 3 → 2,4 = F 3 → 2 + F 3 → 4

F 3 → 2 = F 3 → 2,4 - F 3 → 4

Onde, para o fator de forma F 3 → 2,4 , teremos:

L 3 W = 1 3 = 0,33

L 2,4 W = 2 3 = 0,67

F 3 → 2,4 = 0,32

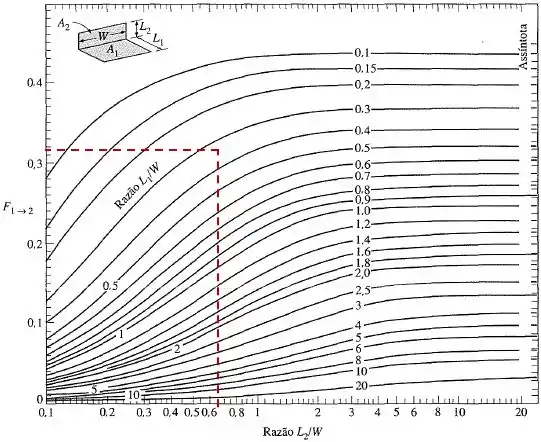
Logo:

F 3 → 2 = F 3 → 2,4 - F 3 → 4 = 0,32 - 0,25

F 3 → 2 = F 1 → 4 = 0,07

Passo 4

Finalmente, o fator de forma F 1 → 2 será:

A 1 + A 3 F 1,3 → 2,4 = A 1 . F 1 → 2 + A 1 . F 1 → 4 + A 3 . F 3 → 2 + A 3 . F 3 → 4

F 1 → 2 = A 1 + A 3 F 1,3 → 2,4 - A 1 . F 1 → 4 - A 3 . F 3 → 2 - A 3 . F 3 → 4 A 1

Onde A 1 = A 3 = 1 × 3 = 3   m 2 . Logo:

F 1 → 2 = 3 + 3 × 0,22 - 3 × 0,07 - 3 × 0,07 - 3 × 0,25 3

Passo 5

( b ) Determine o fluxo de calor radiante entre as placas 1 e 2.

O fluxo de calor é dado por:

q 1 → 2 = σ . T 1 4 - T 2 4 1 - ε 1 ε 1 A 1 + 1 A 2 + 1 - ε 2 ε 2 A 2

Onde:

T 1 = 2000   K

ε 1 = 1

T 2 = 200   K

ε 2 = 0,4

Assim:

q 1 → 2 = 5,67 × 10 - 8 × 2000 4 - 200 4 1 - 1 1 × 3 + 1 3 + 1 - 0,4 0,4 × 3

q 1 → 2 = 1,088 × 10 6   W

Resposta

a F 1 → 2 = F 2 → 1 = 0,05

b q 1 → 2 = 1,088   M W

Exercícios de Livros Relacionados

97 – Irradiação da superfície da terra da atmosfera exibe uma variação espectral forte, principalmente associado com a janela atmosférica na Seção 12.9.2.A) Para uma faixa 0 ≤ λ ≤ 8 μm a emissividade
91 – A radiação solar incidente na superfície da Terra pode ser dividido em componentes direto e difusivo no Problema 12.90. Considere condições para um dia na qual a intensidade da radiação solar dir
A superfície exposta de um amplificador de potência de um receptor utilizado em um satélite terrestre, com área de 130m m por 130m m , tem um revestimento opaco, cinza e difuso, com uma emissividade d
Um disco metálico circular, com diâmetro de 0,4m , é firmemente posicionado contra o solo em uma região estéril, horizontal, onde a terra está a uma temperatura de 280K . A temperatura do céu efetiva
A asa de alumínio oxidado de um avião tem um comprimento de corda deL c =4m e uma emissividade hemisférica espectral caracterizada pela distribuição mostrada na figura.(a) Considere condições nas quai