Uma barreira de radiação difusa e cinza, com de diâmetro e emissividade e nas superfícies interna e externa, respectivamente, é concêntrica a um longo tubo que transporta um fluido de processo quente.
A superfície do tubo é negra e possui diâmetro de . Há vácuo na região interna da barreira. A superfície externa da barreira está exposta a uma grande sala, cujas paredes estão a , e experimenta transferência de calor por convecção com o ar a , com um coeficiente convectivo de .
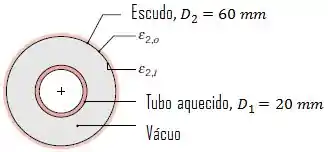
Determine a temperatura de operação do tubo interno se a temperatura da barreira for mantida a .
Passo 1
Fazendo o balando de energia na superfície externa, temos que:
Passo 2
A taxa de transferência de calor entre as superfícies cilíndricas é dada pela seguinte equação tabelada:
A taxa de transferência de calor por convecção será dada por:
A taxa de transferência de calor por radiação entre o tubo externo e a vizinhança será dada por:
Substituindo esses caras na equação que encontramos no Passo 1:
Passo 3
Colocando ordem na casa e isolando a temperatura , teremos:
Substituindo os valores e jogando isso tudo na calculadora, vamos encontrar:
![]()