Em uma plataforma espacial, duas placas de mesmo tamanho são paralelas e estão separadas de . Uma das placas está na temperatura de e a outra na temperatura de .
Essas placas não sofrem incidência solar e o ambiente ao seu redor encontra-se na temperatura de . Para a troca de calor por radiação, o ambiente pode ser representado como uma superfície fictícia, unindo as duas placas e formando a cavidade na forma de um paralelepípedo que é mostrada abaixo.
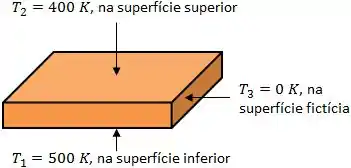
Todas as superfícies são negras. Qual o fluxo de calor por radiação em cada uma das superfícies?
Passo 1
O fluxo de calor em cada superfície é dada por:
Onde as radiosidade são dados por:
Agora temos que descobrir os fatores de forma.
Passo 2
Como as superfícies 1 e 2 são planas:
![]()
O fator de forma entre as superfícies 1 e 2 é dado pelo gráfico abaixo:
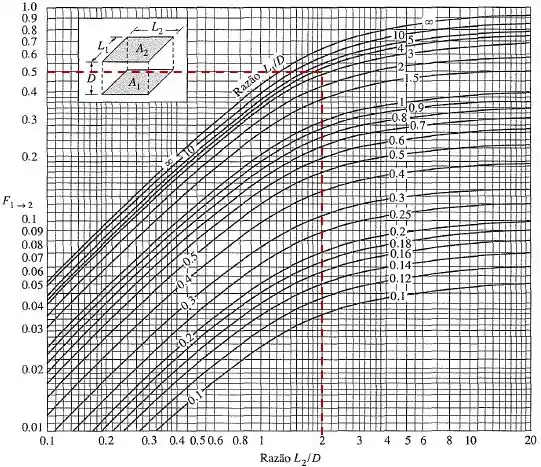
![]()
Utilizando a regra da adição:
![]()
Através da regra da reciprocidade, onde:
Teremos:
![]()
Pela regra da adição:
![]()
Passo 3
Finalmente, os fluxos de calor em cada superfície serão:
![]()
![]()
![]()