A parede de um forno industrial é composta por duas paredes planas verticais distantes e com ar (a ) entre elas. As paredes têm altura igual a e largura igual a . A temperatura da parede 1 é mantida a , e a da parede 2 é mantida a .
A emissividade da parede 1 é igual a e a da parede 2, . Considere as paredes como superfícies cinzas difusas e calcule:
O coeficiente de troca de calor por convecção na parede 1, assumindo que a parede 2 não perturba o escoamento próximo a parede 1.
O calor total perdido pela parede 1.
Considere as seguintes propriedades para o ar: .
Passo 1
O coeficiente de troca de calor por convecção na parede 1, assumindo que a parede 2 não perturba o escoamento próximo a parede 1.
Esse se trata de um problema de convecção natural. Sendo assim, o número de Rayleigh será dado por:
O número de Rayleigh é dado por:
Onde vale:
Assim, substituindo os valores:
Passo 2
Como estamos trabalhando com um caso de placa vertical, para o valor de número de Rayleigh que encontramos, a correlação mais adequada para o número de Reynolds é dada por:
O coeficiente convectivo será:
![]()
Passo 3
O calor total perdido pela parede 1.
O calor total perdido pela parede 1 será a soma do calor perdido por convecção e do calor perdido por radiação . Dessa forma:
Passo 4
O calor perdido por radiação pode ser calculado por:
Onde o fator de forma é obtido a partir do gráfico abaixo, onde:
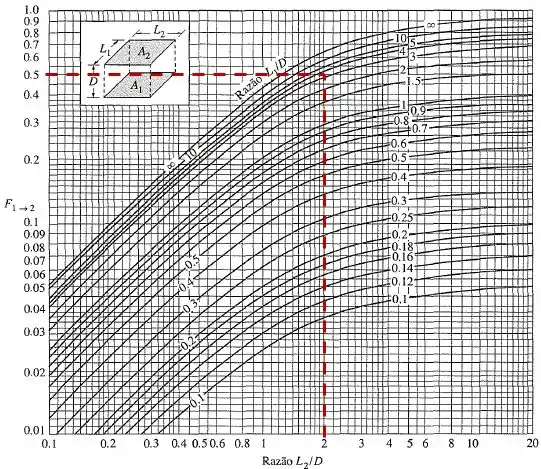
Dessa forma, sendo e :
Assim, o calor perdido pela placa 1 será:
![]()
Resposta