Considere uma longa fenda em forma de com profundidade de , usinada em um bloco mantida a .
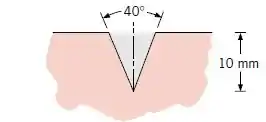
Se as superfícies da fenda são difusas e cinza com uma emissividade de , determine o fluxo radiante que deixa a fenda para a sua vizinhança. Determine também a emissividade efetiva da cavidade.
Passo 1
Uma boa estratégia pra esse tipo de problema é “fechar” a superfície.
Assim, como nós queremos calcular o fluxo radiante que deixa a fenda, vamos idealizar uma superfície que feche a fenda, onde essa superfície é um corpo negro com temperatura . Ou seja, essa superfície irá absorver todo o fluxo de energia.
Fazendo isso e calculando o fluxo térmico entre a fenda e a nossa superfície, vamos estar calculando o fluxo radiante que deixa a fenda.
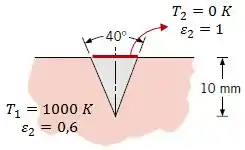
Passo 2
A taxa de radiação emitida pela superfície será dada por:
O fator de forma pode ser calculado através da seguinte relação:
Como a superfície que inventamos é plana, qualquer radiação que ela pudesse emitir jamais incidiria sobre ela mesma, logo:
Pela regra da adição:
Assim:
Como queremos calcular o fluxo radiante, basta dividir toda a expressão pela área que inventamos, logo:
Além disso, como a superfície 2 é negra, , logo:
Passo 3
Em relação às áreas, temos o seguinte:
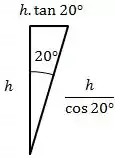
Assim, substituindo os valores:
![]()