Para melhorar o descarte de calor em espaçonaves, um engenheiro propõe fixar uma série de aletas retangulares à superfície externa da espaçonave e cobrir todas as superfícies com um material que se aproxima de um comportamento de corpo negro.
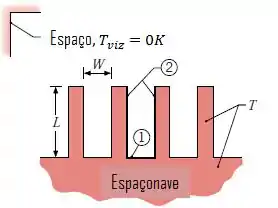
Para superfícies isotérmicas com temperaturas e emissividade , e uma seção em com largura e comprimento , determine a taxa, por unidade de comprimento (normal à página), na qual radiação é transferida de uma seção para o espaço.
Passo 1
A boa pra esse tipo de problema é “fechar” a cavidade.
Assim, vamos imaginar uma superfície que feche a fenda, onde essa superfície é um corpo negro com temperatura , de forma que essa superfície absorva todo o fluxo de energia.
Fazendo isso e calculando o fluxo térmico entre a cavidade e a nossa superfície, vamos estar calculando o fluxo radiante que a deixa.
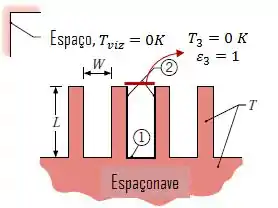
Passo 2
A taxa de radiação que incide na superfície 3 será dada por:
Onde:
Em que é o comprimento da cavidade (na direção normal à página).
Como a superfície que inventamos é plana, nenhuma radiação que ela pudesse emitir incidiria sobre ela mesma, logo:
Pela regra da adição:
Pela regra da reciprocidade:
![]()
Passo 3
Assim:
Como queremos calcular a taxa de transferência de calor por unidade de comprimento, basta dividir toda a equação pelo comprimento , logo:
Além disso, como a superfície 3 é negra, , logo:
Passo 4
Substituindo os valores:
![]()