Considere duas placas paralelas muito grandes com superfícies cinza e difusas.
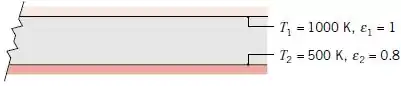
Determine a irradiação na placa superior.
Determine a radiosidade na placa superior.
Qual é a radiosidade da placa inferior.
Qual é a troca líquida de radiação entre as placas por unidade de área das placas?
Passo 1
Determine a irradiação na placa superior.
Sobre a placa superior incide a radiaç��o vinda da placa inferior, e a radiação emitida pela placa superior e que foi refletida pela placa inferior.
Dessa forma:
Substituindo os valores:
![]()
Passo 2
Determine a radiosidade na placa superior.
A radiosidade é definida por
Como a placa superior se trata de um corpo negro, , nenhuma radiação será refletida. Dessa forma:
![]()
Passo 3
Qual é a radiosidade da placa inferior.
No caso da placa inferior, teremos:
A irradiação será composta somente da energia que vem da placa superior, já que a mesma não irá refletir a radiação emitida pela placa inferior. Logo:
![]()
Passo 4
Qual é a troca líquida de radiação entre as placas por unidade de área das placas?
A troca líquida entre as placas pode ser calculada da seguinte forma:
![]()
A mesma ainda poderia ser calculada da seguinte forma:
Resposta